DSB信号调制与解调

DSB

[toc]

理论

DSB 信号调制 theory

DSB 信号（也叫 DSB-SC 信号），DSB 信号调制属于幅度调制

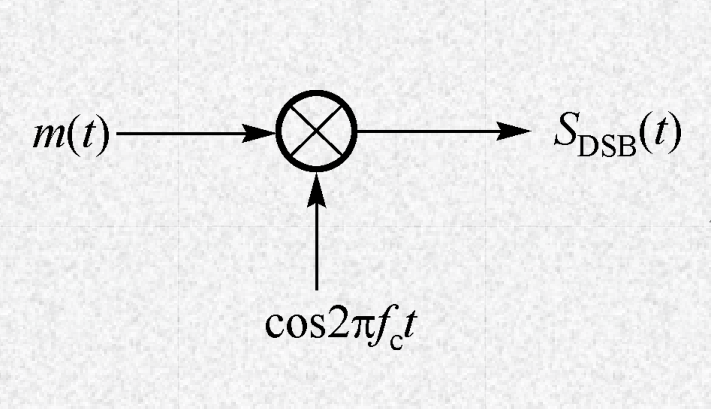
DSB 已调信号：$s_{DSB}(t) = m(t) c(t) = m(t) cos(2 \pi f_c t)$

DSB 已调信号频谱：$S_{DSB}(\omega) = \frac{1}{2}[M(\omega + \omega_c) + M(\omega - \omega_c)]$

DSB 已调信号 $s_{DSB}(t)$ 带宽为基带信号 $m(t)$ 带宽的两倍：$B_{DSB} = 2 f_H$

DSB 信号解调 theory

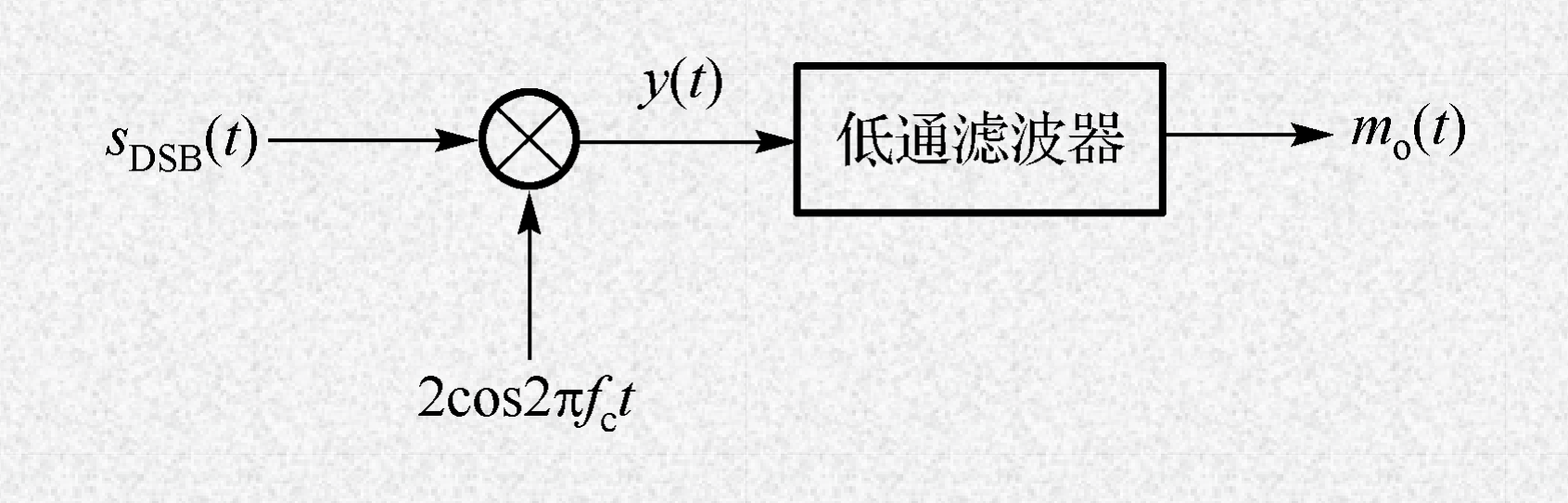
DSB 已调信号只有相干解调

乘法器输出：$y(t) = s_{DSB}(t) \cdot 2cos(2 \pi f_c t) = m(t) [1 + cos(2 \pi 2 f_c t)]$

低通滤波器输出：$m_0(t) = m(t)$（使用低通滤波器，滤掉 $2f_c$ 频率分量即可）

• DSB 信号功率

$P_{DSB} = P_m$

代码

DSB 信号调制 code

clc, clear, clf;
dt = 0.00001;  % 设定步长
T = 0.01;      % 设定时长
t = 0: dt: T - dt;  % 设定时间
%（注：这里范围一定要是 T-dt，而不是 T，否则后面会报错！）

figure(1);

fm = 1000;    % 基带
mt = cos(2 * pi * fm * t);  % 调制信号
subplot(321);
plot(t, mt);
title('调制信号');

[f, sfm] = T2F(t, mt);  % 傅里叶变换：FFT + fftshift
subplot(322);
plot(f, abs(sfm));
title('调制信号频谱');

fc = 10000;   % 载波中心频率
ct = cos(2 * pi * fc * t);  % 载波信号
subplot(323);
plot(t, ct);
title('载波信号');

[f, sfc] = T2F(t, ct);  % 傅里叶变换：FFT + fftshift
subplot(324);
plot(f, abs(sfc));
title('载波信号频谱');

sDSB = mt .* ct;             % DSB 已调信号
subplot(325);
plot(t, sDSB);
title('DSB 已调信号');

subplot(326);
[f, sfdsb] = T2F(t, sDSB);  % 傅里叶变换：FFT + fftshift
plot(f, abs(sfdsb));
title('DSB 已调信号频谱');

DSB 信号解调 code

figure(2);

%% 相干解调
yt = sDSB .* 2 .* ct;  % 乘法器输出
[f, sf] = T2F(t, yt);  % 傅里叶变换
[t_cor_dem_, cor_dem] = lpf(f, sf, 2 * fm);  % 低通滤波，得到相关解调信号
% （注：DSB 信号带宽是基带带宽的两倍！所以低通滤波器输入的截止频率是 2 * fm）
subplot(211);
plot(cor_dem);
title('相干解调信号波形，即原基带信号波形');

subplot(212);
[f, cor_dem_f] = T2F(t_cor_dem_, cor_dem);   % 傅里叶变换：FFT + fftshift
plot(f, abs(cor_dem_f));
title('相干解调信号频谱，即原基带信号频谱');

其他

低通滤波器的其他实现：（以 DSB 信号解调为例）

figure(3);

%% 相干解调
fs = 2^16;
NFFT = 2^16;
f = linspace(-fs/2, fs/2, NFFT);
wc = 2 * pi * 2 * fm / fs;   % 解调器低通滤波器截止频率，2fm
lbf_hn = fir1(32, wc / pi);  % 低通滤波器系统函数，FIR滤波器

yt = sDSB .* 2 .* ct;
Yf = t2f(yt, NFFT);               % 频谱 FFT + fftshift
cor_dem = filter(lbf_hn, 1, yt);  % 相干解调
cor_dem_f = t2f(cor_dem, NFFT);   % 频谱 FFT + fftshift

subplot(211);
plot(t, cor_dem);
title('相干解调信号波形，即原基带信号波形');

subplot(212);
plot(f, abs(cor_dem_f));
title('相干解调信号频谱，即原基带信号频谱');

• 计算功率和能量

% 功率就是对复信号模的平方的平均值
P1 = mean(abs(mt) .^ 2);
P1

% 能量就是P对于时间的积分
E1 = sum(abs(mt ).^ 2 * dt);
E1