AM

[toc]

理论

模拟调制模型：

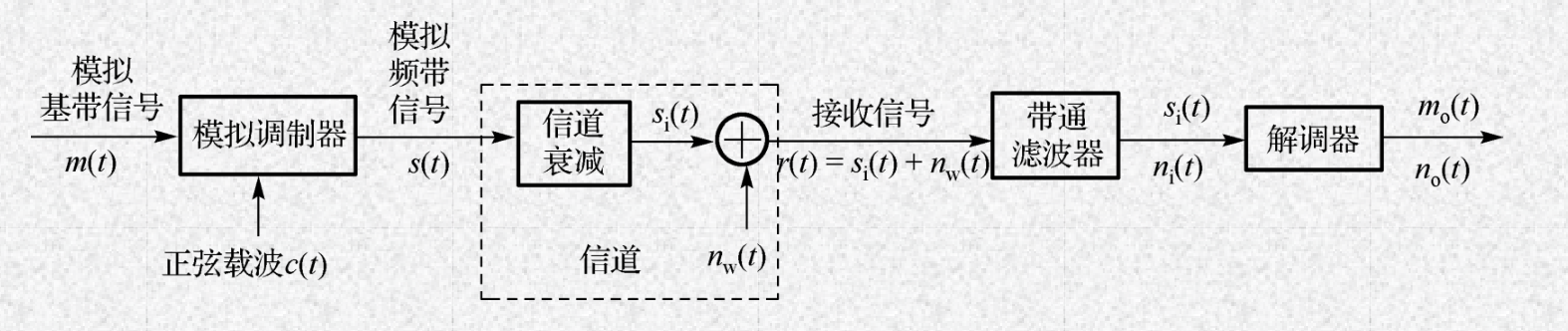
模拟调制模型

其中，模拟基带信号 $m(t) = cos(2 \pi f_m t)$，载波信号 $c(t) = cos(2 \pi f_c t)$

AM 信号调制 theory

AM 信号调制属于幅度调制

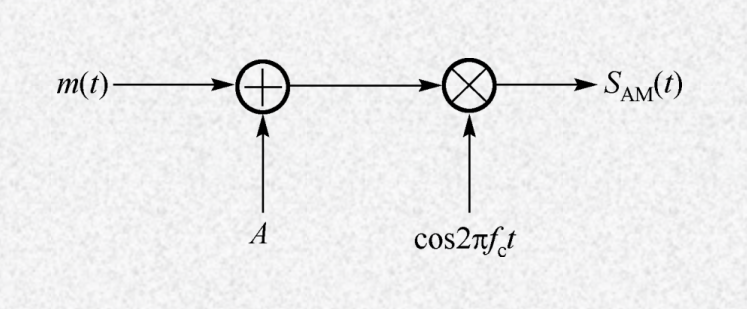
AM信号调制

AM 已调信号：$s_{AM}(t) = [A + m(t)]c(t)$

AM 已调信号频谱：$S_{AM}(\omega) = \pi A [\delta(\omega + \omega_c) + \delta(\omega - \omega_c)] + \frac{1}{2}[M(\omega + \omega_c) + M(\omega - \omega_c)]$

AM 已调信号 $s_{AM}(t)$ 带宽为基带信号 $m(t)$ 带宽的两倍：$B_{AM} = 2 f_H$

AM 信号解调 theory

AM 已调信号解调有两个方法：相干解调、非相干解调（包络检波法）

AM 已调信号解调方法1：相干解调

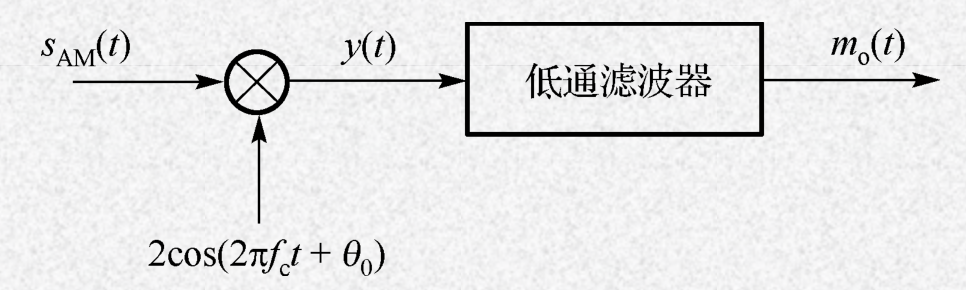
AM已调信号相干解调

其中，一般 $\theta_0 = 0$

step0. 乘法器输出：$y(t) = s_{AM}(t) \cdot 2c(t) = [A + m(t)] c(t) \cdot 2c(t) = (A + m(t)) [1 + cos(2 \pi 2 f_c t)]$
step1. 低通滤波器输出：$m_0(t) = A + m(t)$（使用低通滤波器，滤掉 $2f_c$ 频率分量即可）

AM 已调信号解调方法2：包络检波法

包络检波器原理：（希尔伯特变换）

对于一般信号 $x(t) = A(t) cos(\omega_0 t + \theta(t))$
step1. 求出一般信号的希尔伯特变换：$\hat{x}(t) = H[x(t)] = A(t) sin(\omega_0 t + \theta(t))$
step2. 构造解析信号：$\tilde{x}(t) = x(t) + j \hat{x}(t) = A(t) e^{j \theta(t)} e^{j \omega_0 t}$
step3. 取解析信号的绝对值即可得到原来的一般信号的包络信号：$|A(t)| = |\tilde{x}(t)|$

同理，对于 AM 已调信号 $s_{AM}(t) = [A + m(t)] ct = [A + m(t)] cos(2 \pi f_c t)$
step1. 求出 AM 已调信号的希尔伯特变换：$\hat{m}(t) = H[m(t)] = [A + m(t)] sin(2 \pi f_c t)$
step2. 构造解析信号：$\tilde{m}(t) = m(t) + j \hat{m}(t) = [A + m(t)] e^{j 2 \pi f_c t}$
step3. 取解析信号的绝对值即可得到原来的一般信号的包络信号：$|A + m(t)| = |\tilde{m}(t)|$
step4. 去掉包络信号的直流分量，取包络信号的交流分量，即基带信号：$m(t) = |A + m(t)| - A = A + m(t) - A$

代码

AM 信号的调制 code

clc, clear, clf;
dt = 0.00001;  % 设定步长
T = 0.01;      % 设定时长
t = 0: dt: T - dt;  % 设定时间
%（注：这里范围一定要是 T-dt，而不是 T，否则后面会报错！）

figure(1);

fm = 1000;    % 基带
mt = cos(2 * pi * fm * t);      % 调制信号
subplot(311);
plot(t, mt);
title('调制信号');

fc = 10000;   % 载波中心频率
ct = cos(2 * pi * fc * t);      % 载波信号
subplot(312);
plot(t, ct);
title('载波信号');

A = 1;
sAM = (A + mt) .* ct;           % AM 已调信号
subplot(313);
plot(t, sAM);
title('AM 已调信号');

AM 信号的解调 code

figure(2);

%% 解调方法1：相干解调
yt = sAM .* 2 .* ct;  % 乘法器输出
[f, sf] = T2F(t, yt);  % 傅里叶变换
[t_cor_dem_, cor_dem] = lpf(f, sf, 2 * fm);  % 低通滤波，得到相关解调信号
% （注：AM 信号带宽是基带带宽的两倍！所以低通滤波器输入的截止频率是 2 * fm）
subplot(221);
plot(cor_dem);
title('相干解调信号波形');

m = cor_dem - A;
subplot(223);
plot(m);
title('相干解调信号恢复的原基带信号');

%% 解调方法2：非相干解调（包络检波器）
m_hilbert = hilbert(sAM);  % hilbert 直接得到解析信号，而不是希尔伯特变换！
uncor_dem = abs(m_hilbert);  % 非相干解调信号
subplot(222);
plot(uncor_dem);
title('非相干解调信号波形');

m = uncor_dem - A;
subplot(224);
plot(m);
title('非相干解调信号恢复的原基带信号');

其中，用到 T2F() 和 lpf() 两个自定义的函数，以及 hilbert() 一个 MATLAB 内置函数，函数说明如下：