第3章-放大器频率特性基础
[toc]
3.1 放大器频率特性的基本概念
一般,放大器中含有电抗元件。在多频率的模拟信号激励下,因频率不同,放大器的增益会随之改变,因此,在正弦稳态情况下,增益必须采用复数表示,即复增益:
复增益:${\large A(j\omega)=A(\omega)e^{j\phi_A(\omega)}}$
幅频特性:${\large A(\omega)}$;相频特性:${\large \phi_A(\omega)}$
或者
复增益:${\large A(jf)=A(f)e^{j\phi_A(f)}}$
幅频特性:${\large A(f)}$;相频特性:${\large \phi_A(f)}$
相应的,可以画出幅频特性曲线和相频特性曲线。
大的耦合电容认为短路,小的极间电容认为开路。耦合电容是高通,极间电容是低通;所以高频要考虑极间电容,低频考虑耦合电容。
我们认为,当放大器增益下降到最大增益的 $\frac{1}{\sqrt{2}}$ 时,对应了两个频率,分别为上限截止频率 $f_H$ 和 下限截止频率 $f_L$,这两个频率之间的频率就是放大器的通频带,在这个频率范围内,我们近似认为放大器的增益是一个常数,即通频带以内,放大器的增益无失真。
在频率很高和频率很低的时候出现的失真是由于线性电抗元件引起的,称之为线性失真(频率失真)。
频率失真包括幅频失真和相频失真,线性失真的特点:不产生新的频率成分。
非线性失真:功率放大器的交越失真、放大器的饱和失真和截止失真
3.2 频率特性的稳态描述方法及波特图坐标系
波特图,即幅频特性曲线和相频特性曲线
幅频和相频特性波特图的横坐标均采用对数坐标(横坐标没有 $0$)
相频特性曲线的纵坐标 $\varphi_H(f)$ 采用传统的比例坐标
幅频特性曲线的纵坐标 $A_v(f)(dB)$ 采用对数坐标,$A_v(f)(dB) = 20lgA_v(f) = 20lg|A_v(jf)|$
3.3 一阶低通和高通RC滤波器的渐近波特图
什么是一阶?:一个独立动态元件
- 一阶低通 RC 滤波器
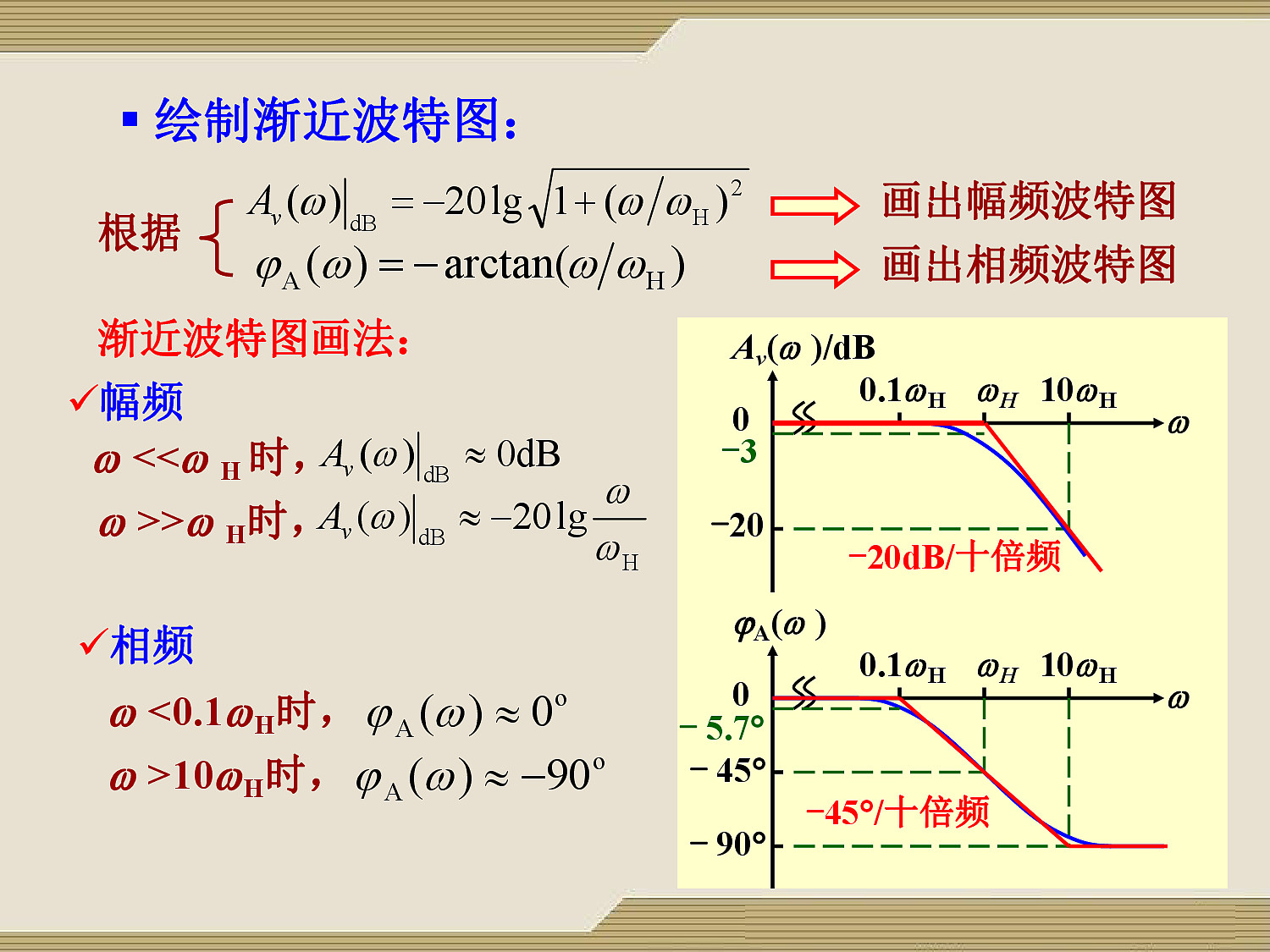
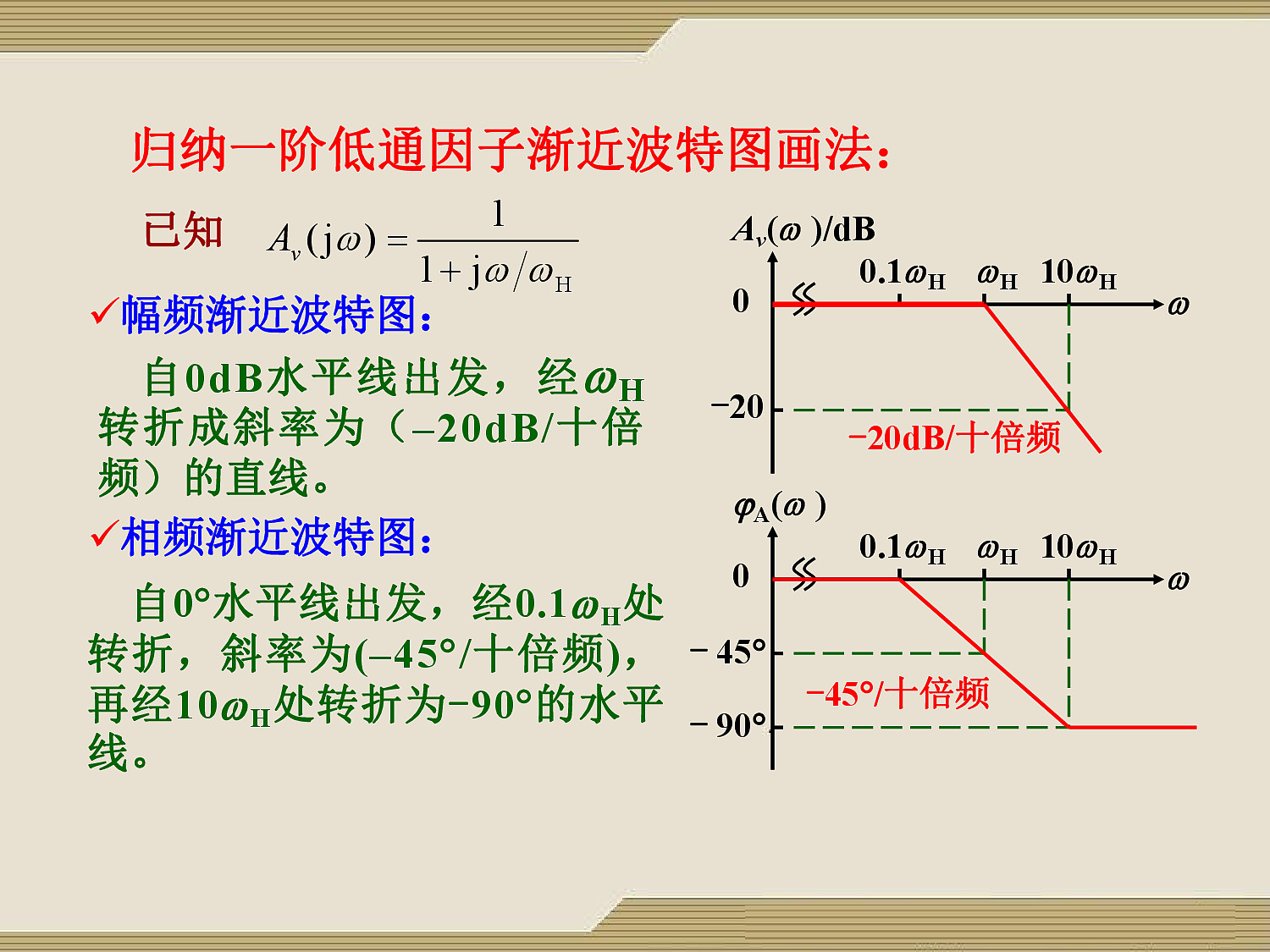
${\large A_v(j\omega) = \frac{1}{1 + j\frac{\omega}{\omega_H}}},~ \omega_H = \frac{1}{RC}$
幅值:$A_v(j\omega)|_{dB} = -20log\sqrt{(1 + (\frac{\omega}{\omega_H})^2)}$
相角:$\varphi_A(\omega) = -arctan\frac{\omega}{\omega_H}$
波特图:
幅频渐进波特图:从 $\omega_H$ 开始,-20dB/10倍频
相频渐进波特图:从 $0.1\omega_H$ 开始,-45°/10倍频

- 一阶高通 RC 滤波器
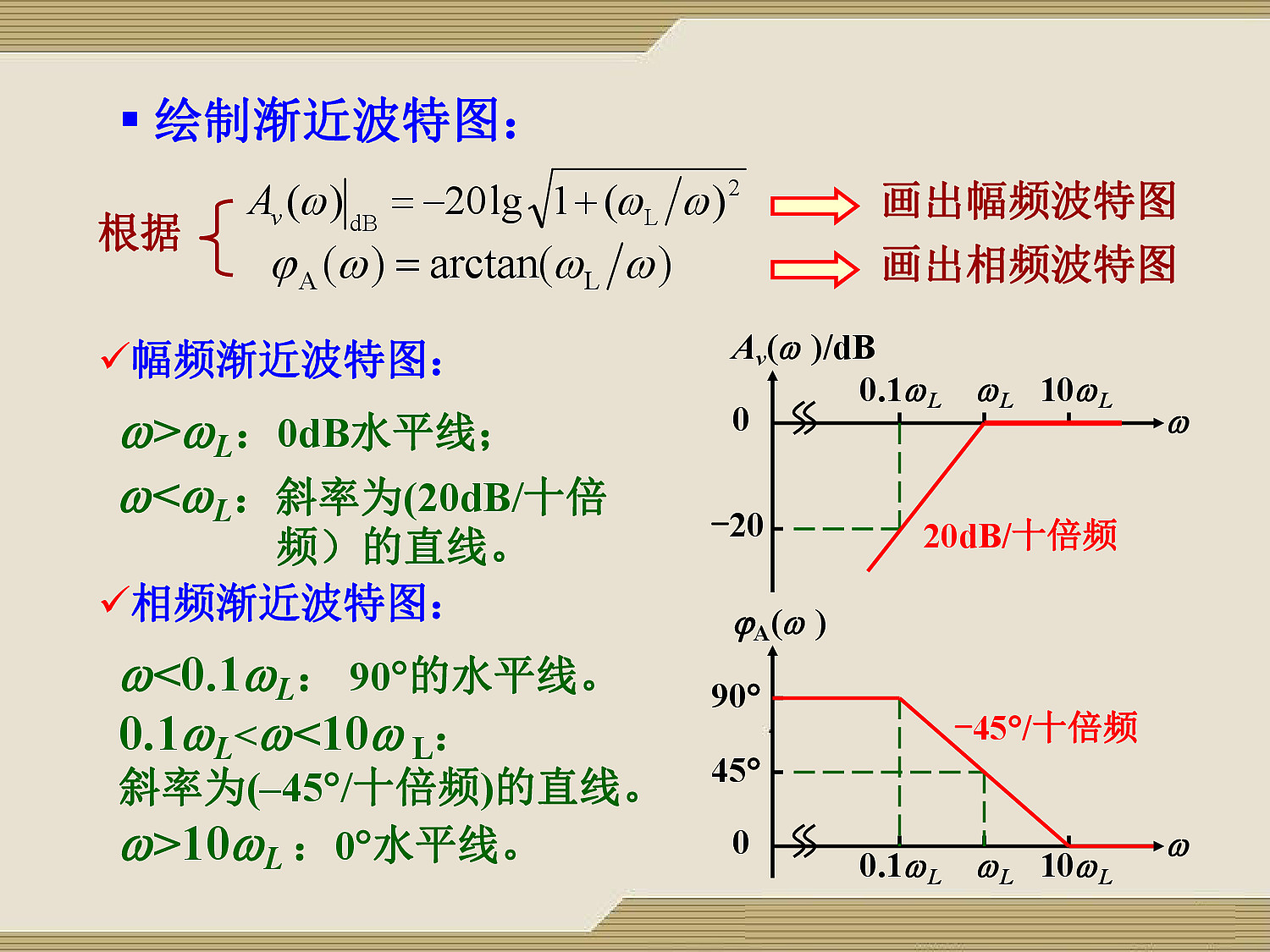
${\large A_v(j\omega) = \frac{1}{1 - j\frac{\omega_L}{\omega}}},~ \omega = \frac{1}{RC}$
幅值:$A_v(j\omega)|_{dB} = -20log\sqrt{(1 + (\frac{\omega_L}{\omega})^2)}$
相角:$\varphi_A(\omega) = arctan\frac{\omega_L}{\omega}$
波特图:
幅频渐进波特图:从 $\omega_L$ 之前,20dB/10倍频
相频渐进波特图:从 $0.1\omega_L$ 开始,-45°/10倍频

3.4 多因子增益的渐近波特图画法
- RC 高通电路波特图的另解
已知:${\large A_v(j\omega) = (j\frac{\omega}{\omega_H})(\frac{1}{1 + j\frac{\omega}{\omega_H}})}$
幅值:${\large A_v(\omega)|_{dB} = [20lg\frac{\omega}{\omega_H}] + [20lg\sqrt{\frac{1}{1 + (\frac{\omega}{\omega_H})^2}}]}$
相角:${\large \varphi_A(\omega) = [90°] + [-arctan\frac{\omega}{\omega_H}]}$
因此,波特图可以由各个低通/高通因子叠加形成。
- 例:${\large A_v(j\omega) = \frac{1000}{(1 + j\frac{\omega}{\omega_{H1}})(1 + j\frac{\omega}{\omega_{H2}})}}$
幅频:(1)$20lg1000 = 60dB$(2)$20lg\frac{1}{\sqrt{1 + (\frac{\omega}{\omega_{H1}})^2}}$(3)$20lg\frac{1}{\sqrt{1 + (\frac{\omega}{\omega_{H2}})^2}}$
相角:(1)$0°$(2)$-arctan\frac{\omega}{\omega_{H1}}$(3)$-arctan\frac{\omega}{\omega_{H2}}$
- 耦合大电容、旁路大电容是高通因子
- PN 结结电容 $C_{b’e}$ 和 $C_{b’c}$ 是低通因子
- $C_{b’c}$ 势垒电容
- $C_{b’e}$ 扩散电容:$C_{b’e} \gg C_{b’c}$
增益:${\large A_v(jf) \approx = \frac{A_{vm}}{(1 - j\frac{f_{L1}}{f})\cdots(1 - j\frac{f_{Ln}}{f})(1 + j\frac{f}{f_{H1}})\cdots(1 + j\frac{f}{f_{Hm}})}}$
$n$ 为独立耦合、旁路大电容个数,$m$ 为 PN 结结电容个数。
上限截止频率:$f_H \approx 1 / (\frac{1}{f_{H1}} + \cdots + \frac{1}{f_{Hm}}) = 1 / (2 \pi (\tau_{1} + \cdots + \tau_{m}))$
下限截止频率:$f_L \approx f_{L1} + \cdots + f_{Ln}$
一般来说,放大器级数越多,其中的电容越多,通频带越窄。
3.5 晶体管的高频小信号电路模型和频率特性参数

共发射电路:
截止角频率:$\omega_\beta = \frac{1}{rC} = \frac{1}{r_{b’e}(C_{b’e} + C_{b’c})}$
其中,势垒电容(手册有):$C_{b’c}$
放大倍数(复数):$\beta(j\omega) = \frac{I_c(j\omega)}{I_b(j\omega)}|{{V_{ce}=0}} \approx \frac{\beta}{1+j\frac{\omega}{\omega_\beta}}$
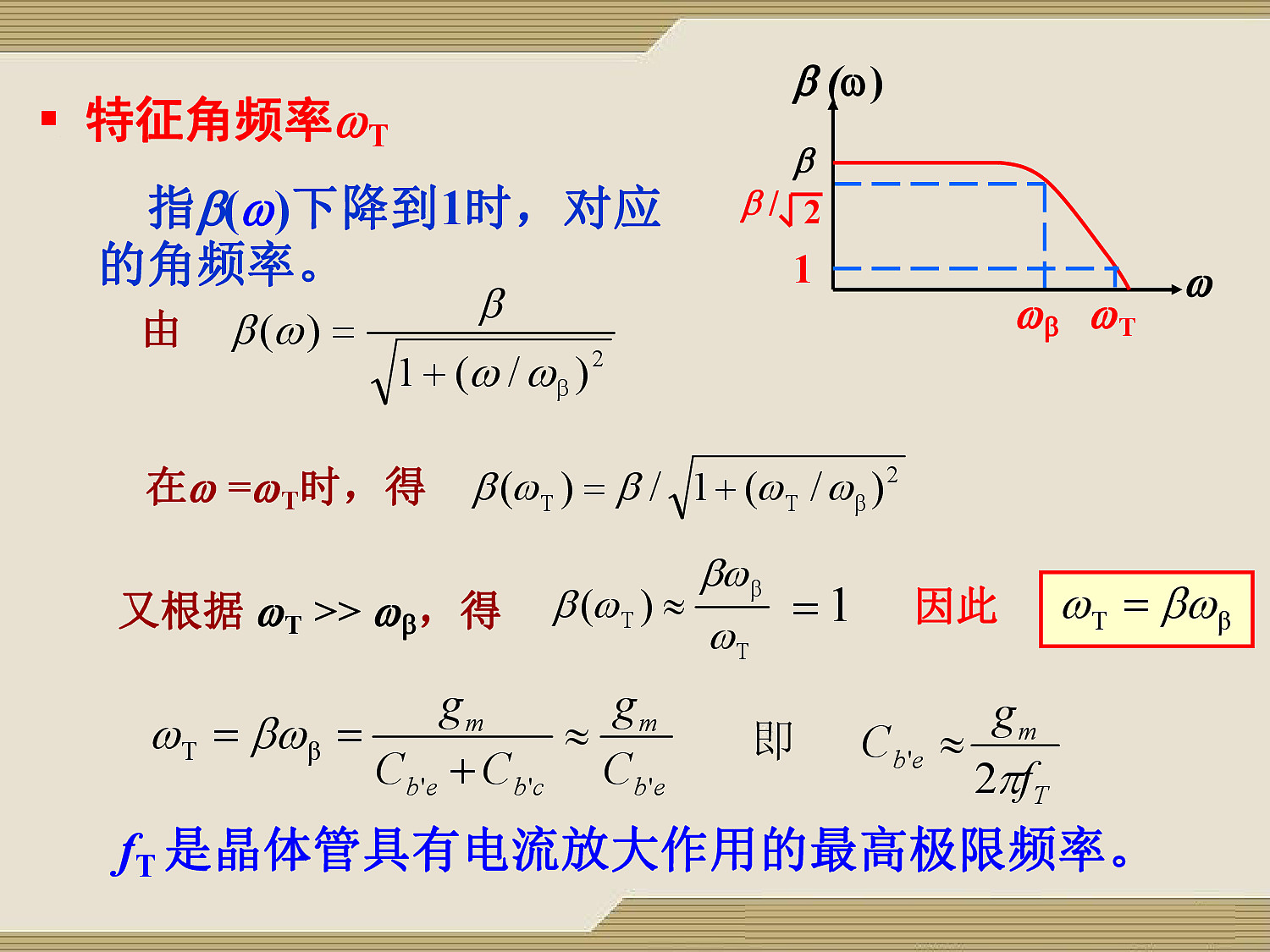
故,放大倍数:$\beta(\omega) = \beta / \sqrt{1 + (\omega_T / \omega_\beta)^2}$
特征角频率:$\omega_T = \beta \omega_\beta \approx g_m r_{b’e}\frac{1}{r_{b’e}C_{b’e}} = \frac{g_m}{C_{b’e}}$
特征频率(手册有):$f_T = \omega / 2 \pi = \frac{g_m}{2 \pi C_{b’e}}$
故,扩散电容:$C_{b’e} \approx \frac{g_m}{2 \pi f_T}$
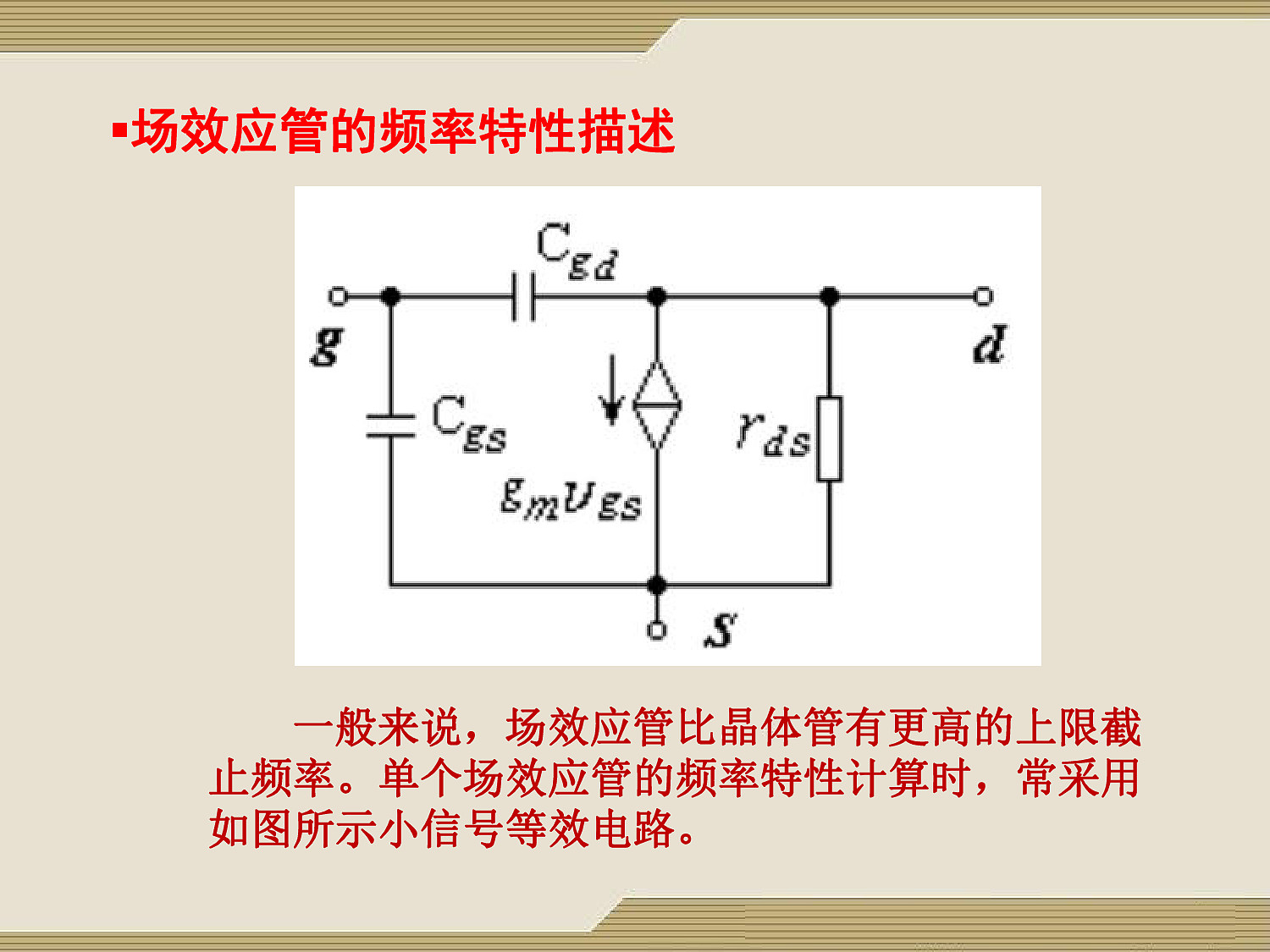
场效应管的频率特性描述
3.6 共发射极放大器高频频率特性分析(密勒等效)
1.jpg)
2.jpg)
3.jpg)
密勒定理:
$C_1 = C[1 - A(j\omega)]$
$C_2 = C[1 - {\large \frac{1}{A(j\omega)}}]$
密勒定理:
①电容模拟电感
②小电容模拟大电容
共发射极放大电路:
增益:$A(j\omega) \approx -g_mR_L’$
4.jpg)
5.jpg)
6.jpg)
有一项:$R_tg_mR_L’C_{b’c}$,远大于其他项,说明 $C_{b’c}$ 对上限截止频率更大一些。
3.7 共发射极放大器频率特性工程近似分析

工程近似:
低频:求其他电容短路戴维南等效电阻 $R_n$
高频:求其他电容开路戴维南等效电阻 $R_m$
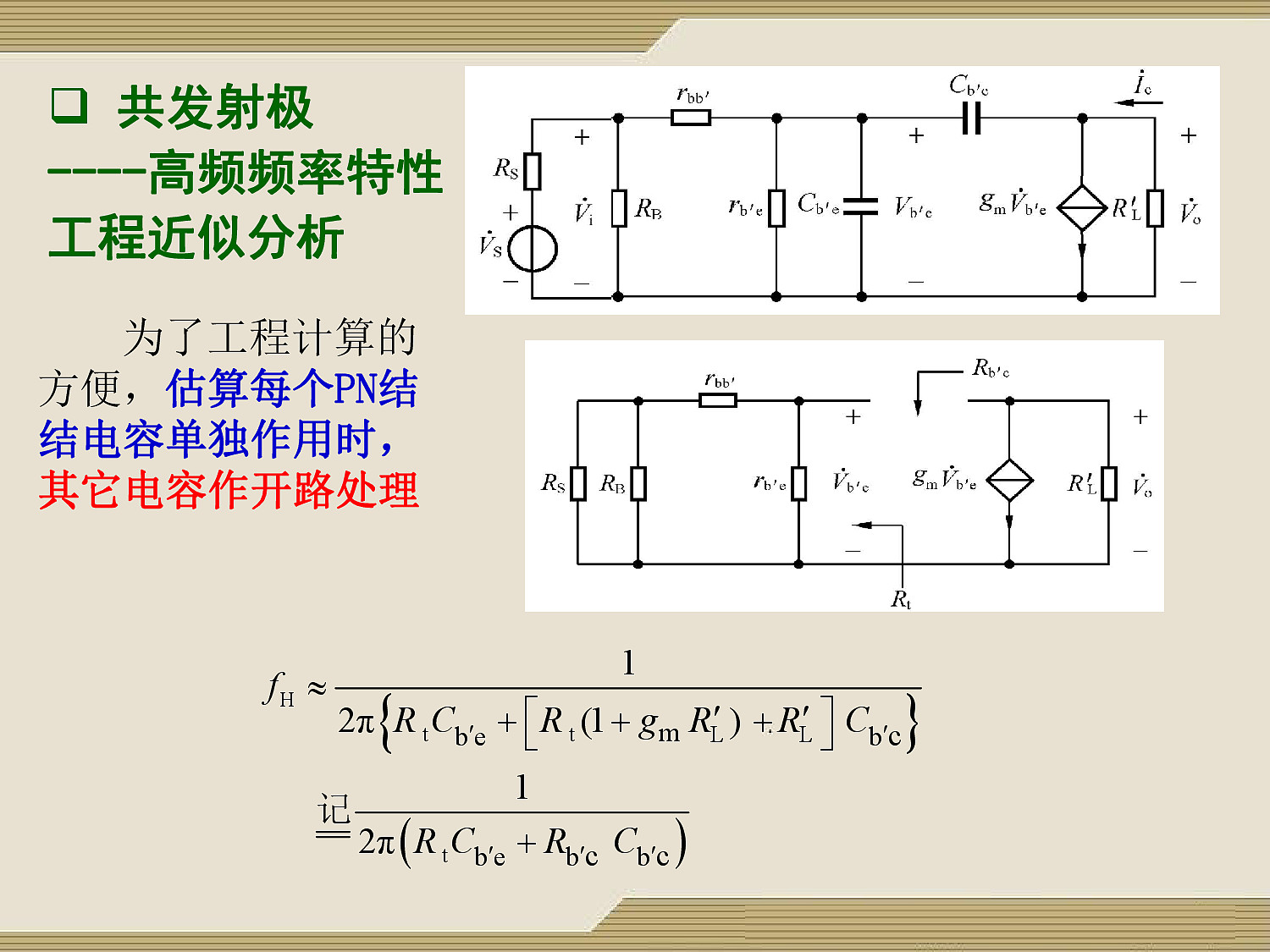
高频:$f_H \approx 1 / [2 \pi (R_tC_{b’e} + R_{b’c}C_{b’c})]$
$R_t = [(R_S // R_B) + r_{bb’}] // r_{b’e}$
$R_{b’c} = R_t + (1 + g_mR_t)R_L’$
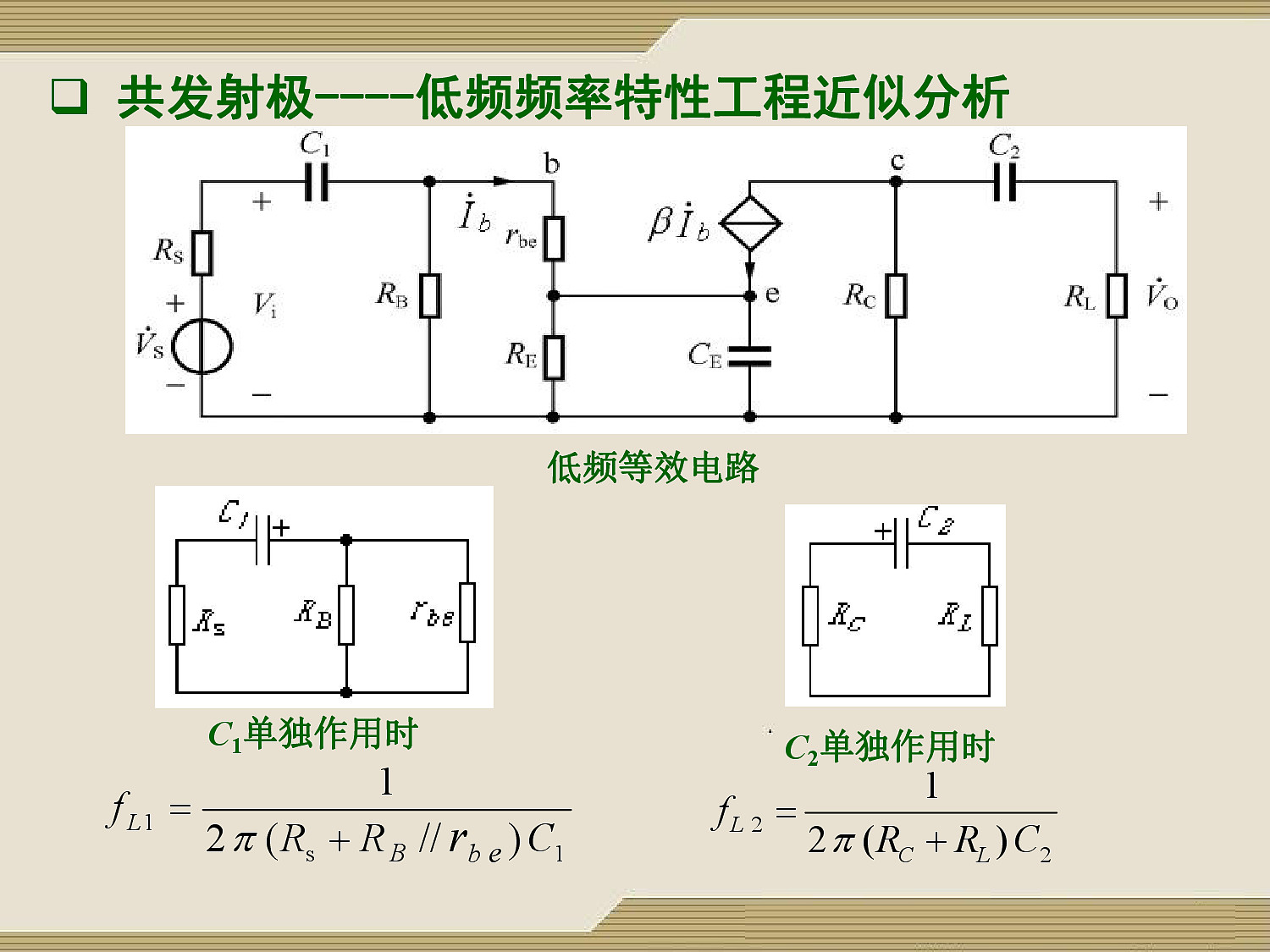
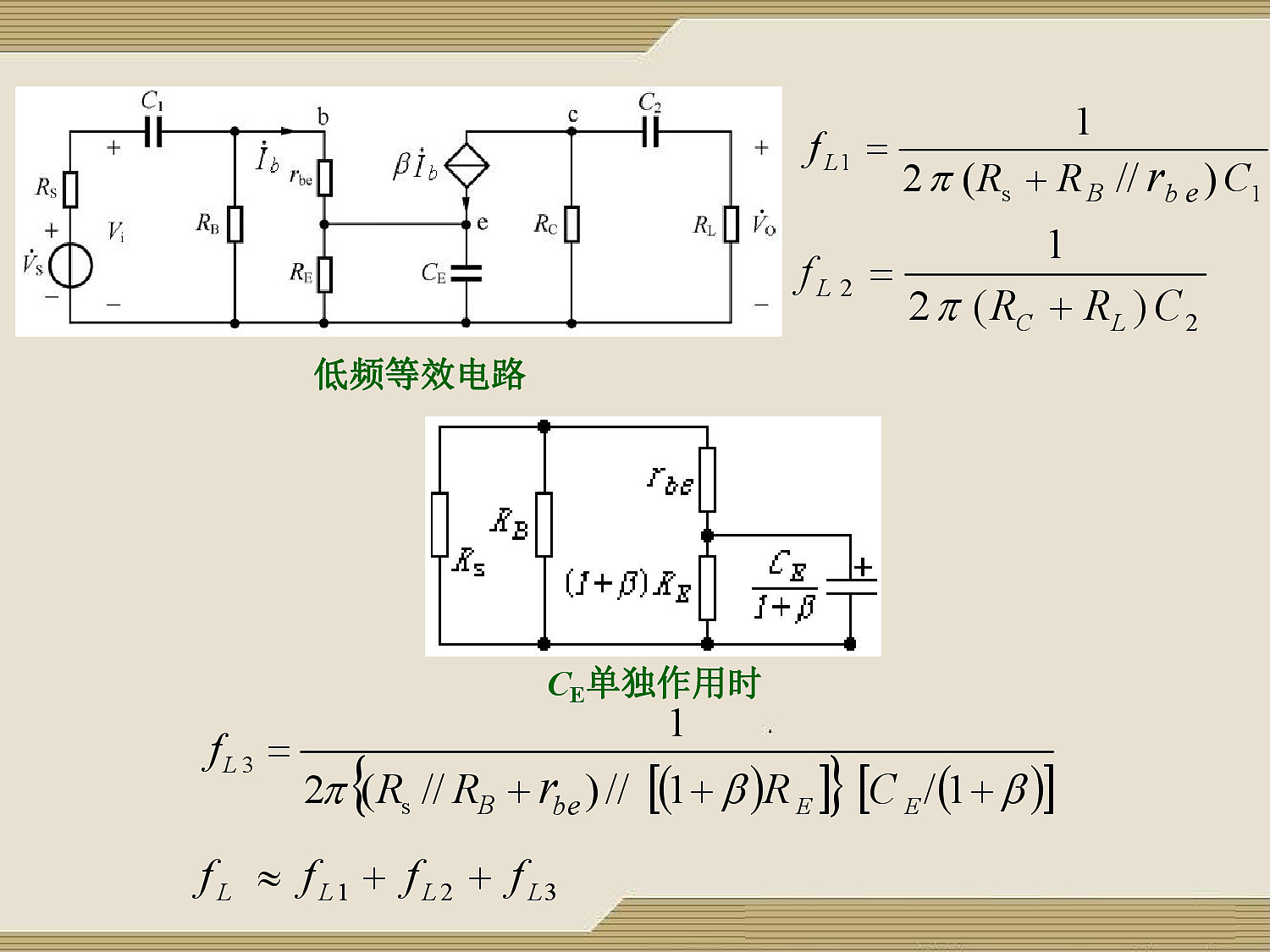
低频:$f_L \approx f_{L1} + f_{L2} + f_{L3} \approx f_{L3}$
$f_{L3} \gg f_{L1} + f_{L2}$
旁路电容 $C_E$ 对放大器的低频特性影响最大

增益带宽积和放大器的增益没有太大关系,即在共发射极放大器里面,信号源和晶体管确定之后,增益带宽积近似为一个常数。
提高增益带宽积:使用好的信号源(理想电压源:信号源内阻小)、好的晶体管($r_{bb’} 小、C_{b’c} 小、f_T 高$)



