第1章-半导体基础元件于非线性电路

模电
模电笔记
发布日期:   2022-06-29
更新日期:   2022-08-17
文章字数:   3.7k
阅读时长:   14 分
阅读次数:  

第1章-半导体基础元件于非线性电路

[toc]

$大_{大} V_D：直流量，常数（手册有）$

$小_{小} i_d：交流量$

$大_{小} V_{im}：交流有效值 幅值$

$小_{大}：交流直流之和的瞬时总量，（既有直流又有交流）$

1.1 本征半导体

半导体：导电能力介于导体和绝缘体之间的一种物质。（常见半导体材料：硅晶体、锗晶体、砷化镓化合物等）

一个硅原子会与四个相邻的硅原子形成共价键结构。

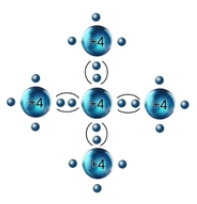
本征半导体：纯净的、不含杂质(纯度$99.9999999%$)的半导体

共价键的束缚力很强，当热力学温度为零度，而且没有其他外界能量激发的时候，价电子全部会束缚在共价键中，晶格中没有自由移动的载流子，所以此时的半导体不导电，相当于绝缘体。

本征激发：当温度升高/光照加强时，会产生自由电子空穴对这种现象。

自由电子（热激发产生）和空穴（价电子挣脱束缚后留下的空位）是成对出现的，称为自由电子空穴对。

自由电子带负电荷，可自由移动；空穴带与电子等量的正电荷，也可移动。

空穴的移动反映了价电子的移动，价电子移动方向与空穴移动反向相反。即，空穴能自由移动而参与导电。这样，可以用空穴移动产生的电流代表价电子移动产生的电流。可以把空穴看成一种可移动的带电粒子。

载流子：参与导电的粒子。半导体中有两种载流子：自由电子和空穴。

复合：自由电子和空穴相遇而同时消失。外部条件不变时，载流子的产生和复合处于动态平衡之中。

1.2 杂质半导体

半导体中的热敏性、光敏性、参杂性

热敏性：温度升高，导电能力显著提高
光敏性：光照加强，导电能力显著变化
参杂性：本征半导体加入杂质，导电能力显著提高

本征半导体 –加杂质元素–> 杂质半导体

掺入少量杂质元素产生的空穴/自由电子数目远大于本征激发产生的载流子数目

添加的杂质主要是三价/五价元素：硼 B、磷 P 等

  • P型半导体（+3价杂质，如 B）

三价杂质接收电子 -> 受主杂质

杂质元素 –常温电离–> $\begin{cases}空穴（可以自由移动，参与导电）\\ 负离子（不能自由移动，不参与导电）\end{cases}$

P型半导体（空穴半导体）$\begin{cases}多子——空穴（产生：杂质电离(主要) + 本征激发）\\ 少子——自由电子（产生：本征激发）\end{cases}$

P半导体简化模型表示：

  • N型半导体（+5价杂质，如 P）

五价杂质接收电子 -> 施主杂质

杂质元素 –常温电离–> $\begin{cases}自由电子（可以自由移动，参与导电）\\ 正离子（不能自由移动，不参与导电）\end{cases}$

N型半导体（电子半导体）$\begin{cases}多子——自由电子（产生：杂质电离(主要) + 本征激发）\\ 少子——空穴（产生：本征激发）\end{cases}$

N半导体简化模型表示：

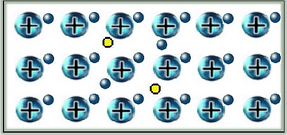
杂质半导体呈电中性$\begin{cases}多子浓度主要取决于参杂浓度\\ 少子浓度取决于本征激发\end{cases}$

1.3 PN结及其单向导电性

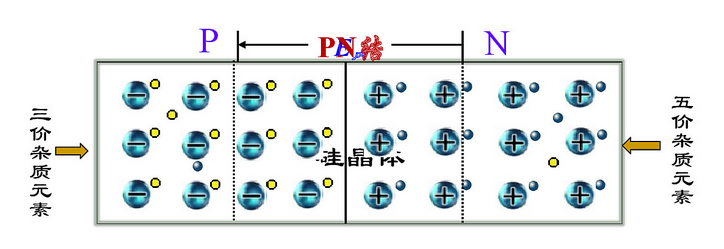
  • PN结正偏特性：正向导通

呈小电阻特性，理想情况下相当于开关闭合，处于导通状态。

外电场与内电场方向相反，内建电场减弱 -> 多子扩散 -> 多子向PN结移动，中和部分离子 -> 阻挡层(耗尽层)变窄 -> 多子扩散形成扩散电流 -> PN结导通

电压 $V_D$ 略微升高，电流 $i_D$ 显著升高

导通电压：$V_{D(on)} \approx \begin{cases}0.7V & (Si)\ 0.2V & (Ge)\end{cases}$

  • PN结反偏特性：反向截止

呈大电阻特性，理想情况下相当于开关断开，处于截止状态。

外电场与内电场方向相同，内建电场增强 -> 少子漂移 -> 多子背离PN结移动，中和部分离子 -> 阻挡层变宽 -> 少子漂移形成扩散电流 -> PN结截止

  • PN结单向导电的伏安特性

1.4 二极管简介

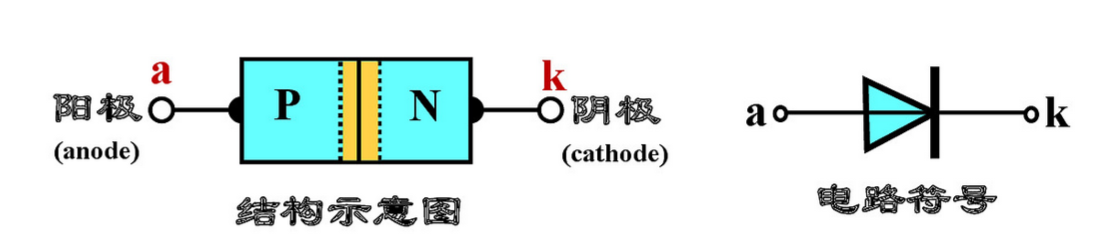
常见封装形式的二极管：有特殊色环/色带对应的电极是阴极

  • 二极管的特性

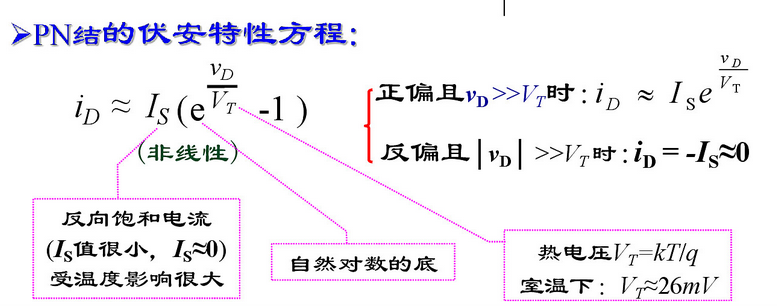
伏安特性方程：${\large i_D \approx I_S (e^{\frac{\nu_{D} }{V_{T} } } - 1)}$
此方程只描述单向导电特性、温度特性和电容特性。

开启电压/门坎电压(二极管$\approx$0.5V，Si 0.7V，Ge 0.2V)：只有正偏电压超过一定电流值时，电流才明显增加。

  • 硅二极管的伏安特性曲线：正向特性、反向特性、反向击穿特性

二极管的正向压降近似等于导通电压，反向电流近似为反向饱和电流

1.5 二极管简化模型

工程上，使用二极管的简化模型代替其指数模型——使用分段线性

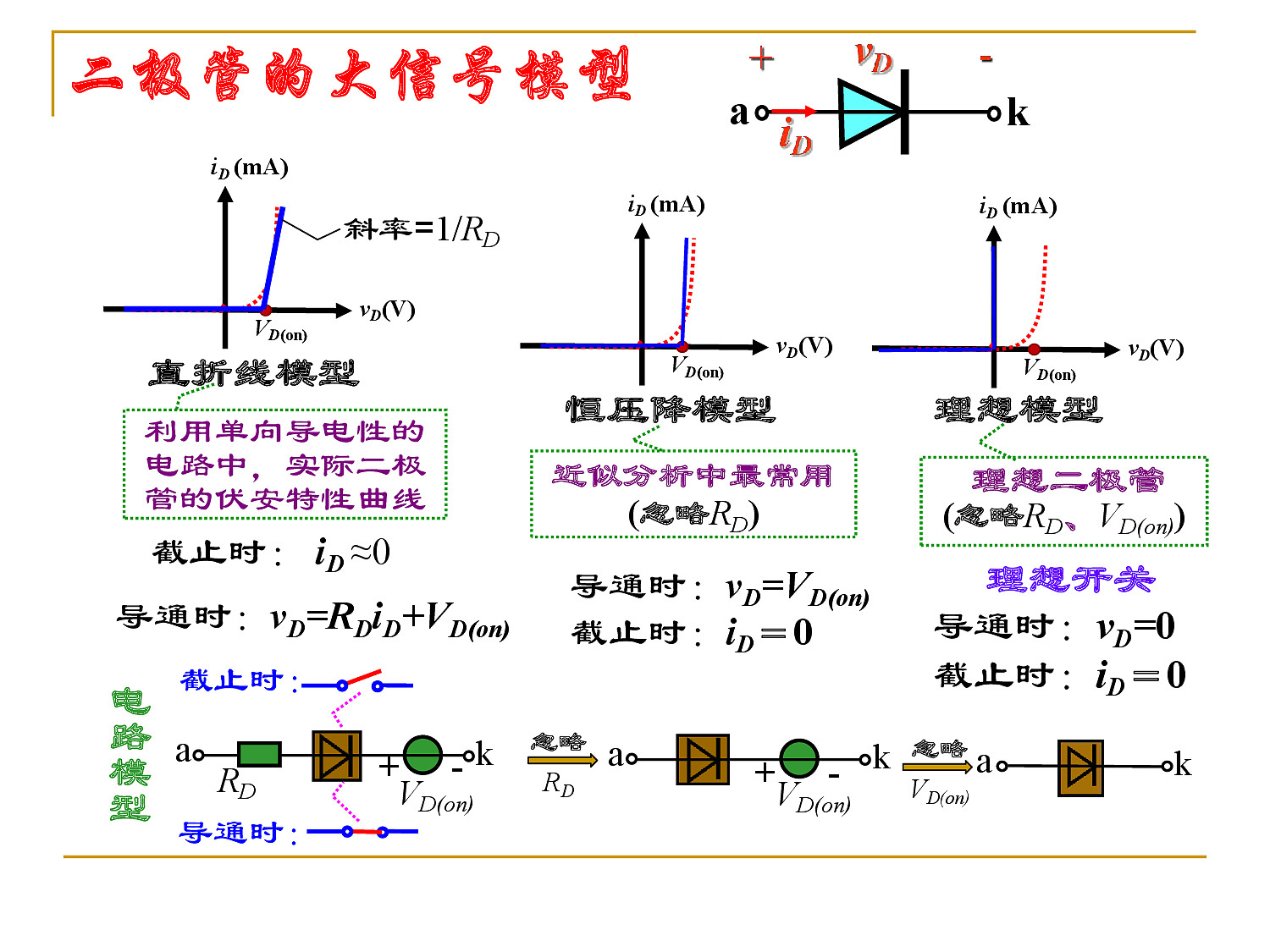
  • 二极管的几种简化模型

    • 直折线模型
    • 恒压降模型
    • 理想模型
    • 小信号模型（前三种都是打信号模型）

  • 大信号模型建模思路：使用分段线性方法，把二极管非线性关系近似表示为几段线性关系。

    • 大电压大电流工作的等效模型
    • 只反映二极管的单向导通型
    • 关键判断二极管是导通还是截止

  • 小信号模型

    • 高频工作时，还需考虑二极管的结电容特性

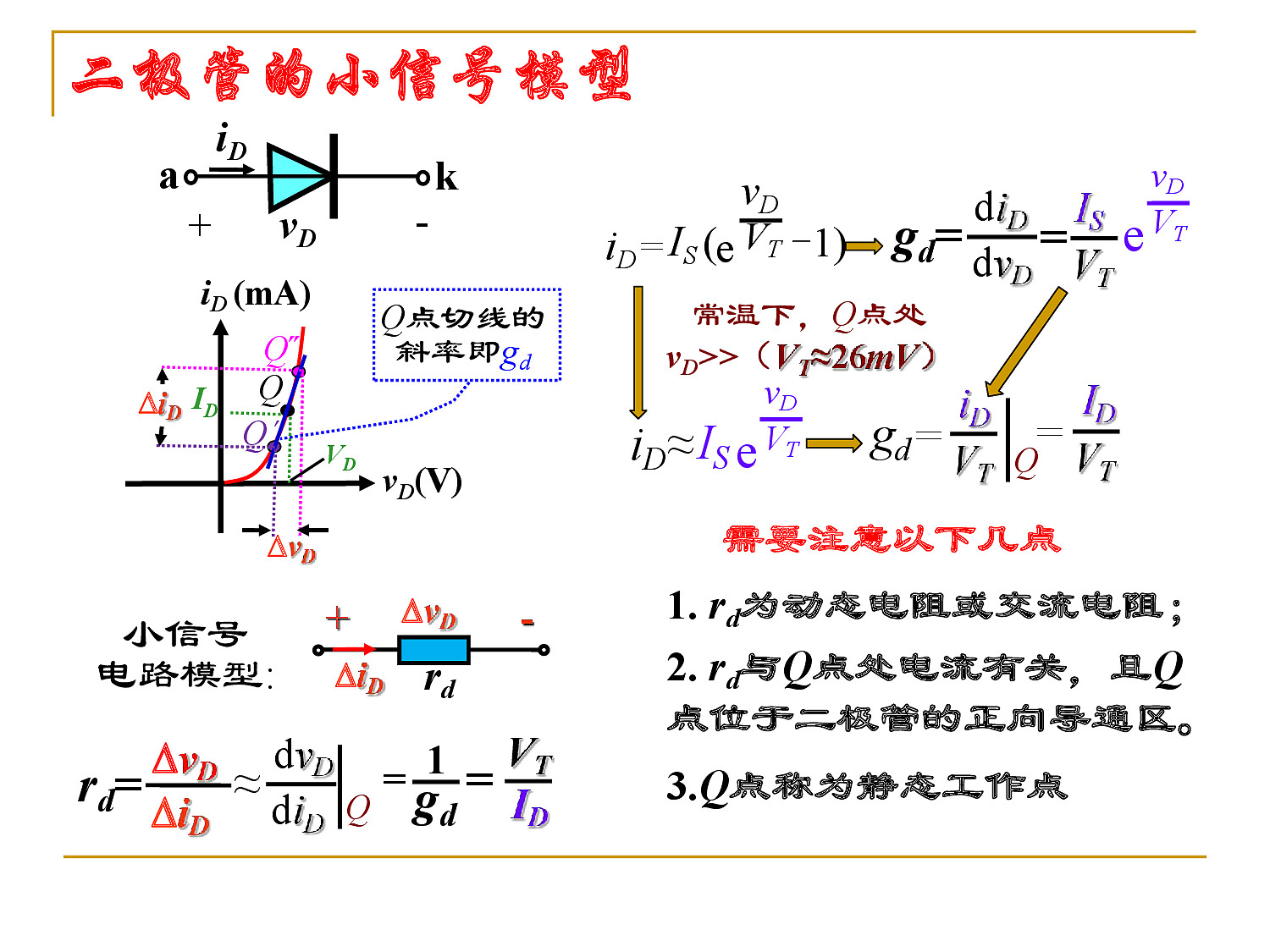
工程上，使用简化模型分析、设计二极管电路，但是最终工程实现和电路优化时，使用复杂模型进行精度误差分析。

根据二极管的伏安特性曲线和方程：二极管的动态电阻 $r_d$ 随着加在其两端的电压增大而增大。

1.6 二极管应用电路之整流电路

若电路中有多个二极管，正偏电压最大的二极管优先导通

  • 判断二极管导通/截止

理想二极管：$V_D > 0$ 导通，反之截止
实际二极管：$V_D > V_{D(on)}$ 导通，反之截止

当电路中有多个二极管时，正偏电压最大的管子优先导通，其余管子需要重新分析其工作状态。

  • 半波整流电路

使用二极管的理想模型分析电路

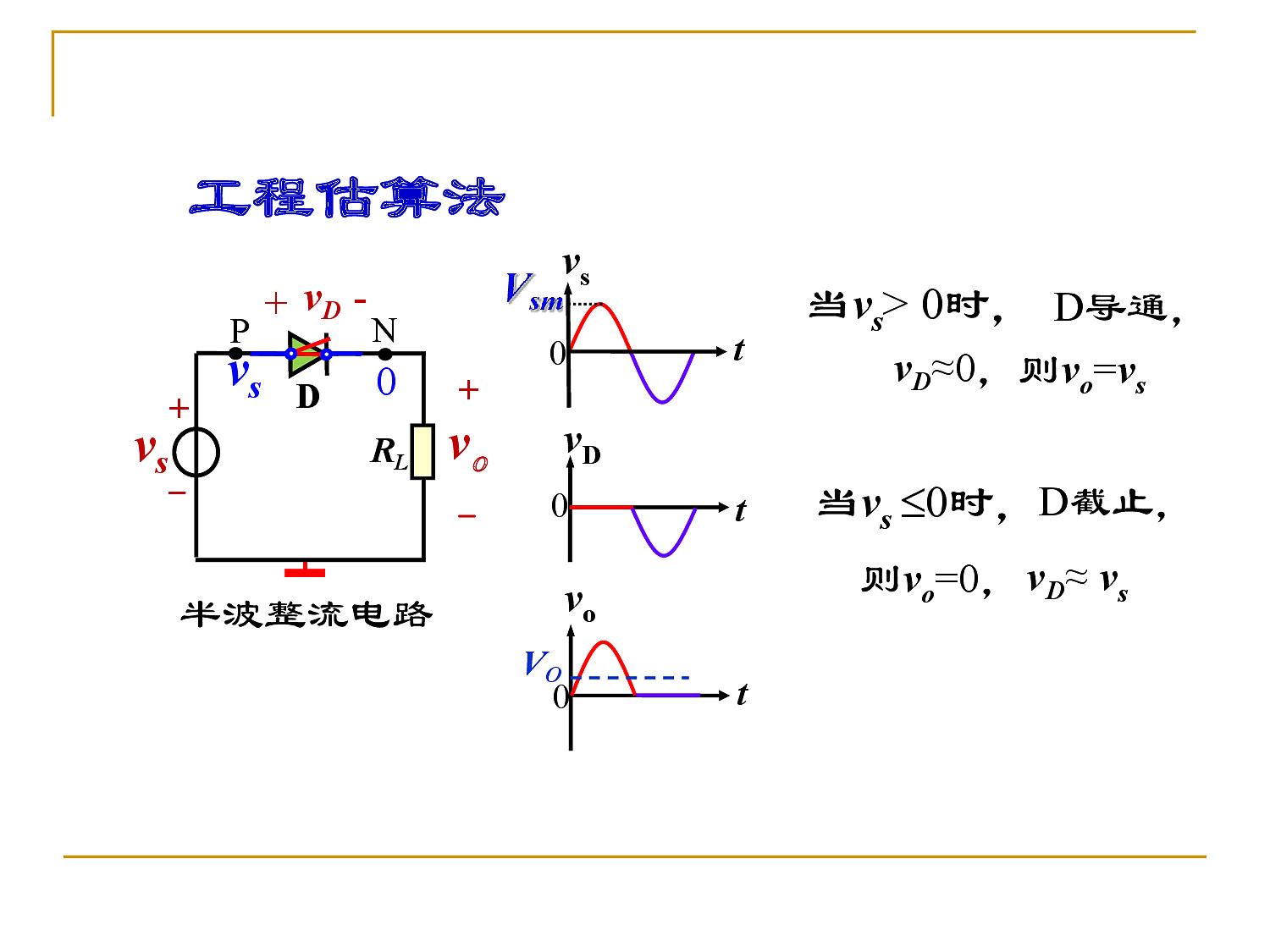
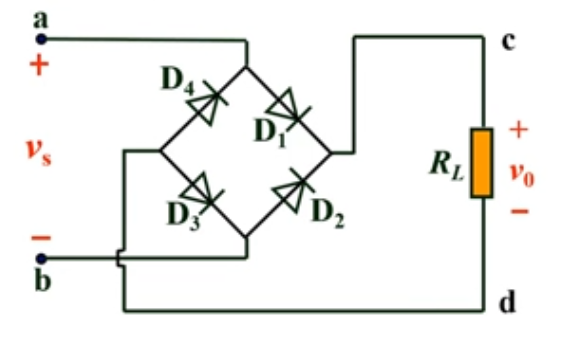
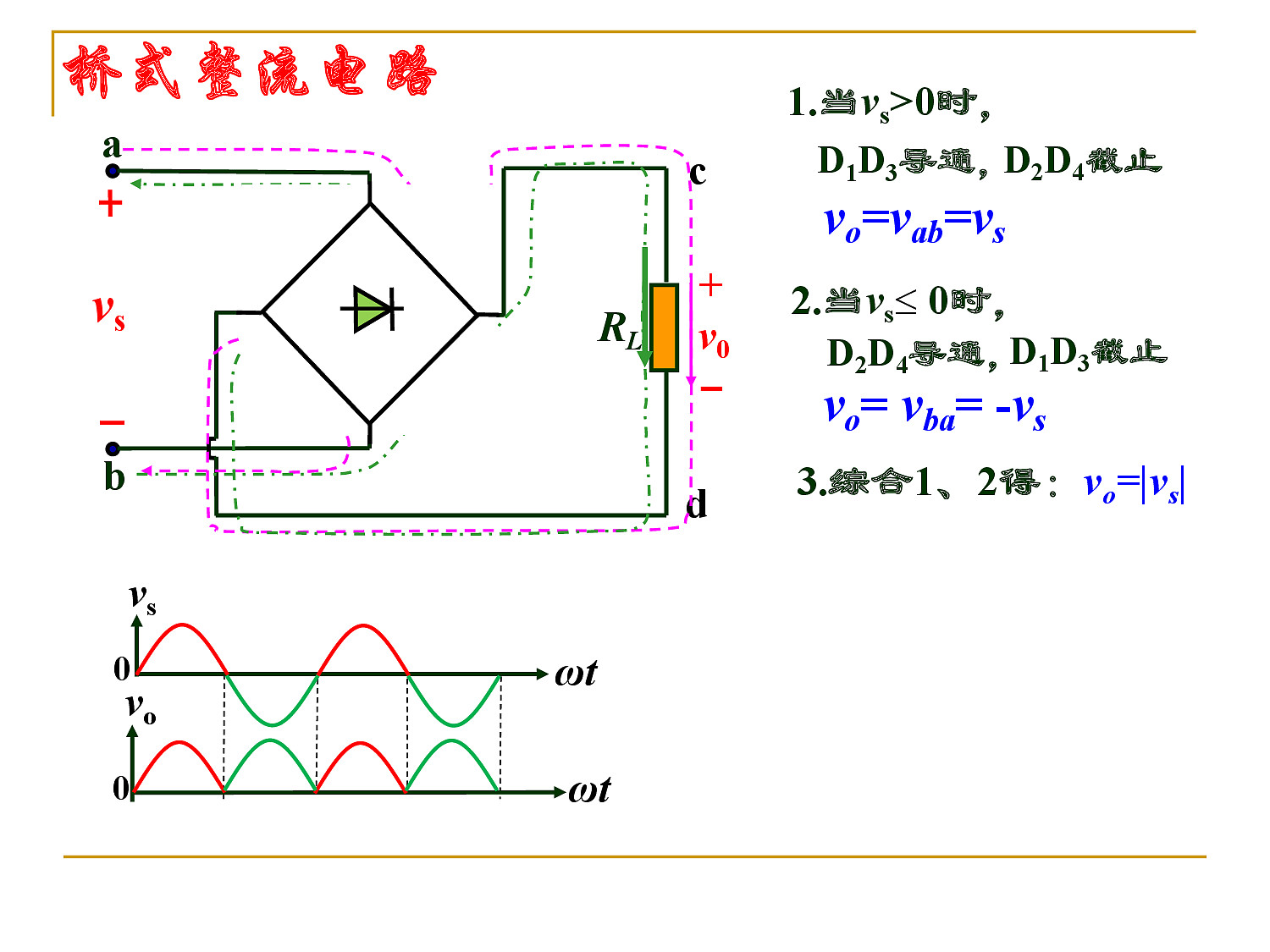
  • 桥式整流电路

使用二极管的理想模型分析电路

1.7 二极管应用之限幅电路及开关电路

  • 限幅电路
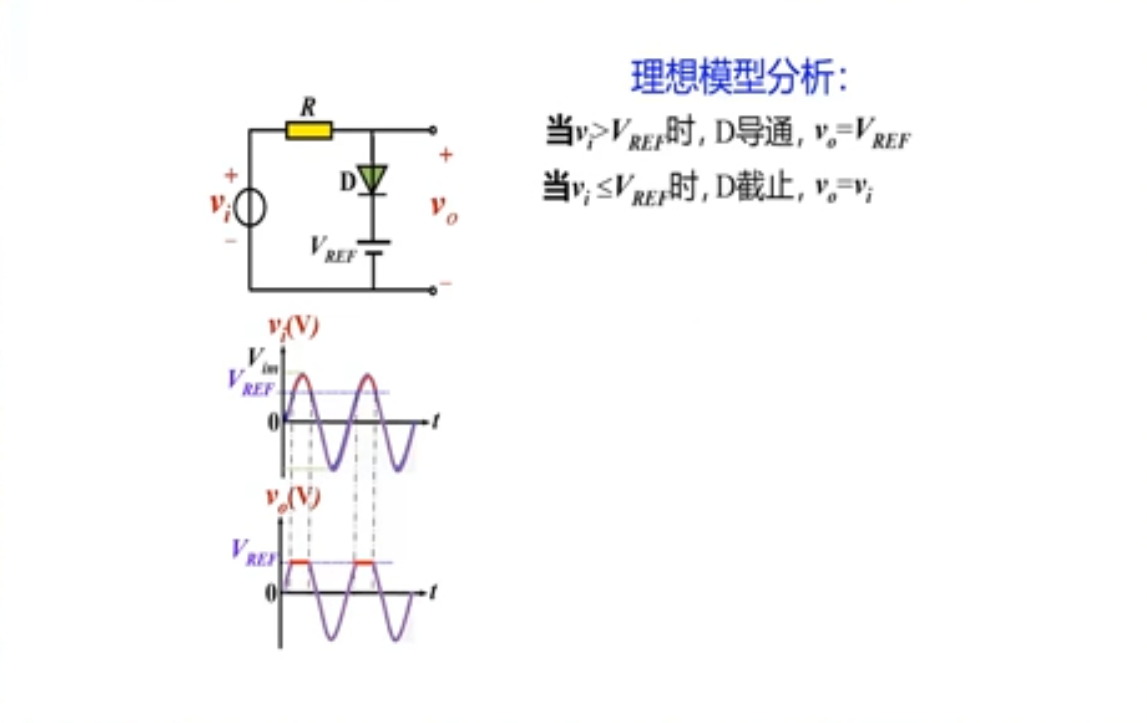
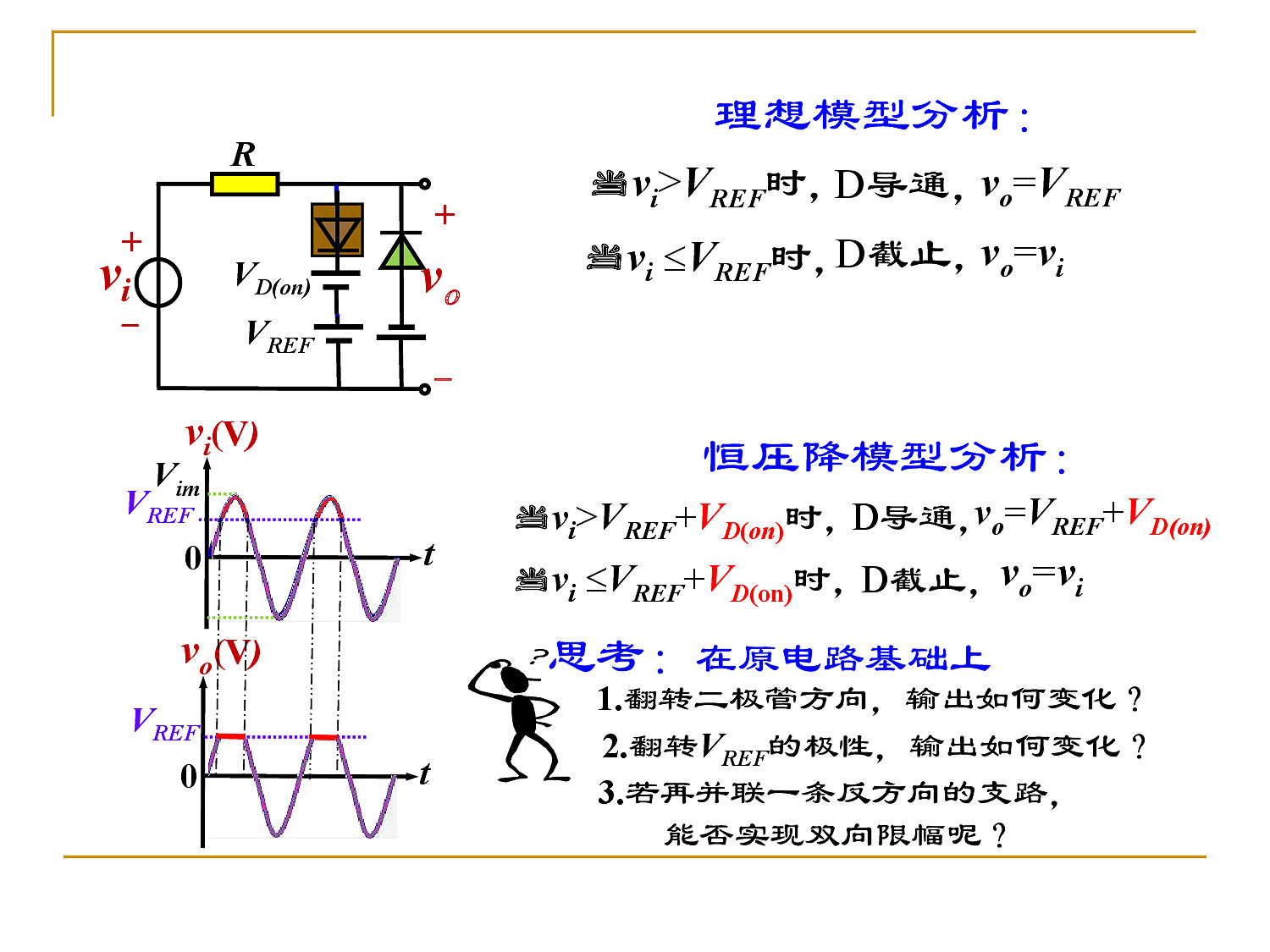
  • 开关电路

设：二极管的导通电压为$V_{D(on)}=0.7V$

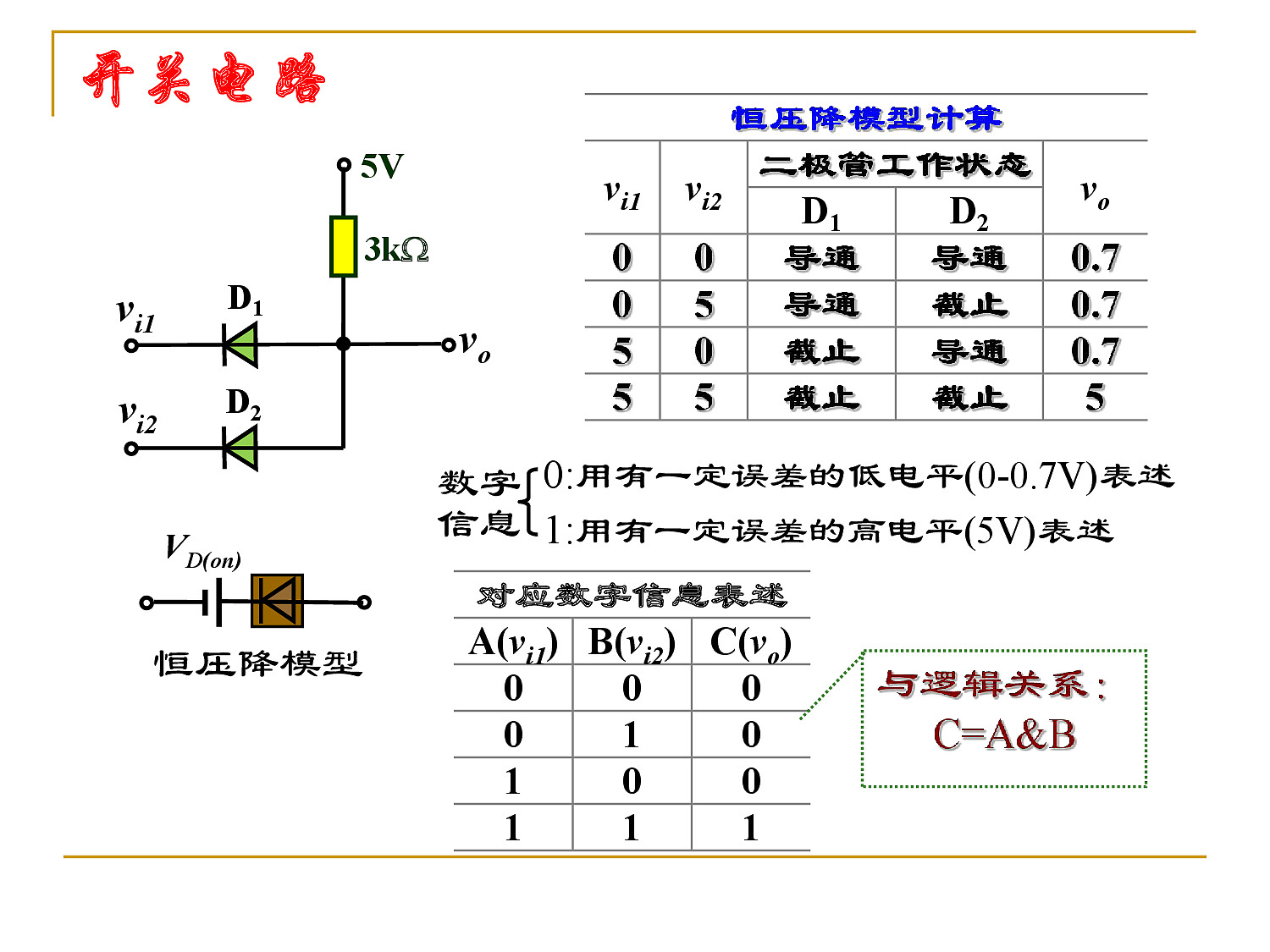
1.8 二极管的小信号应用

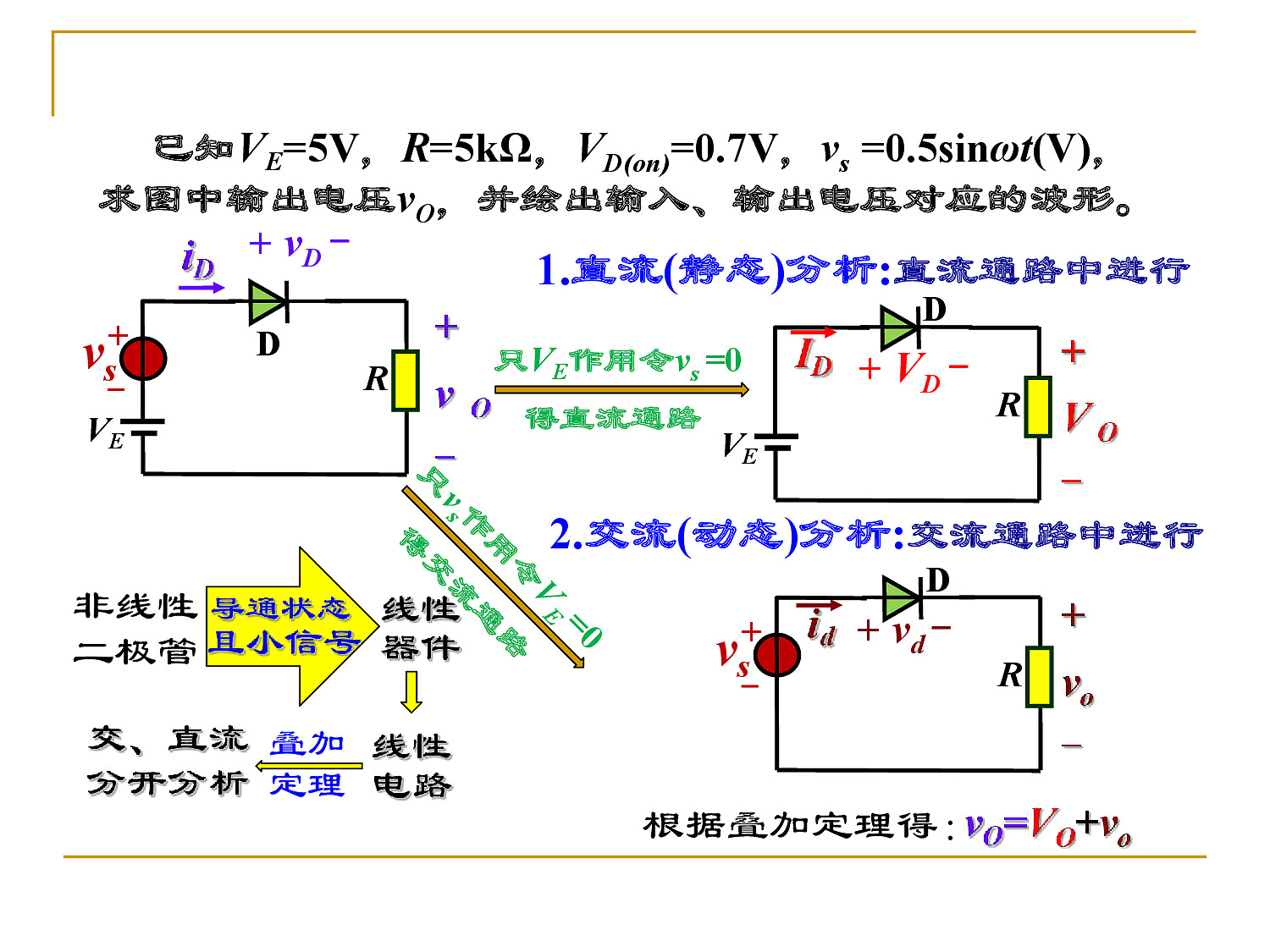
  • 等效电路法
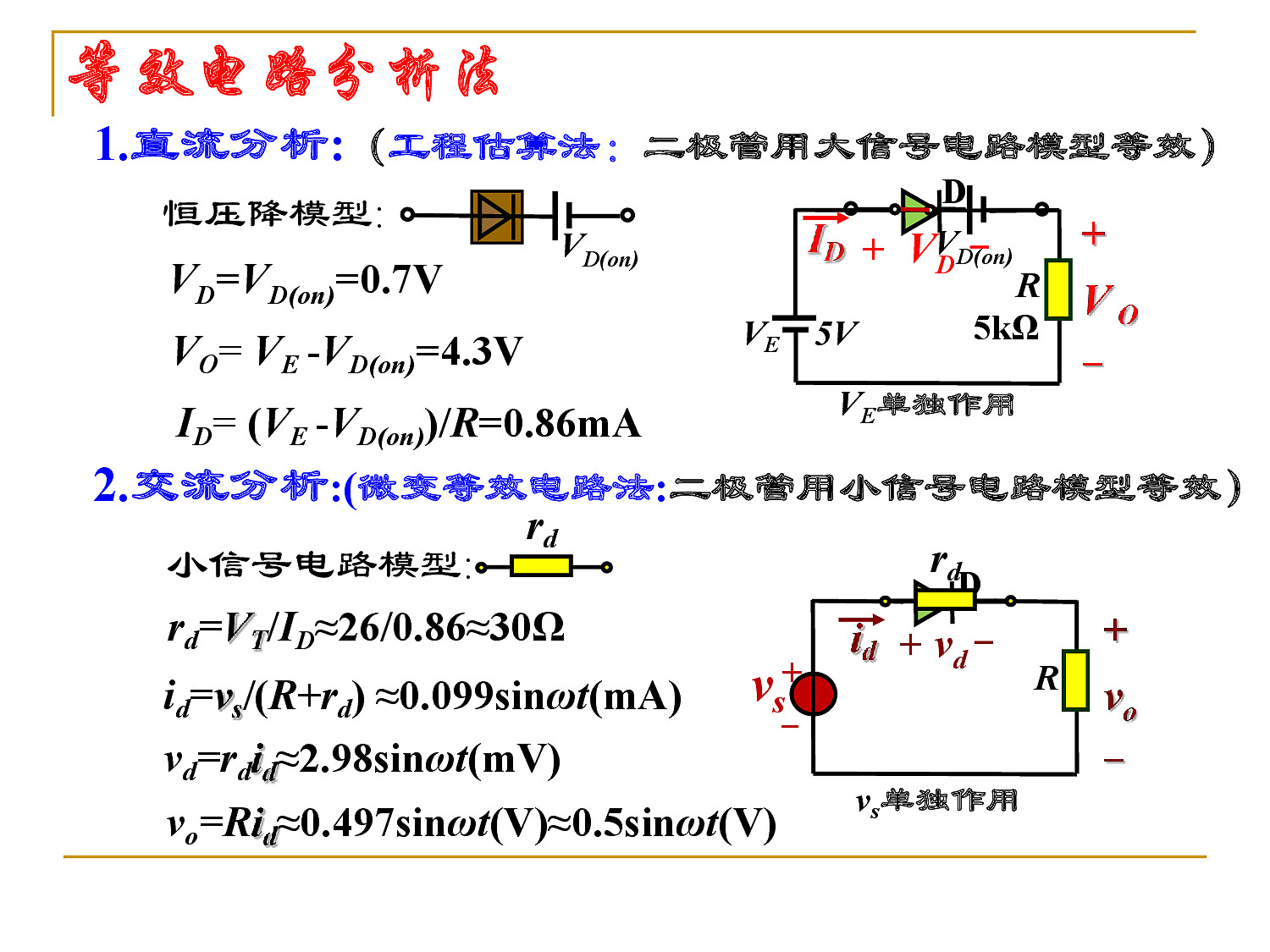
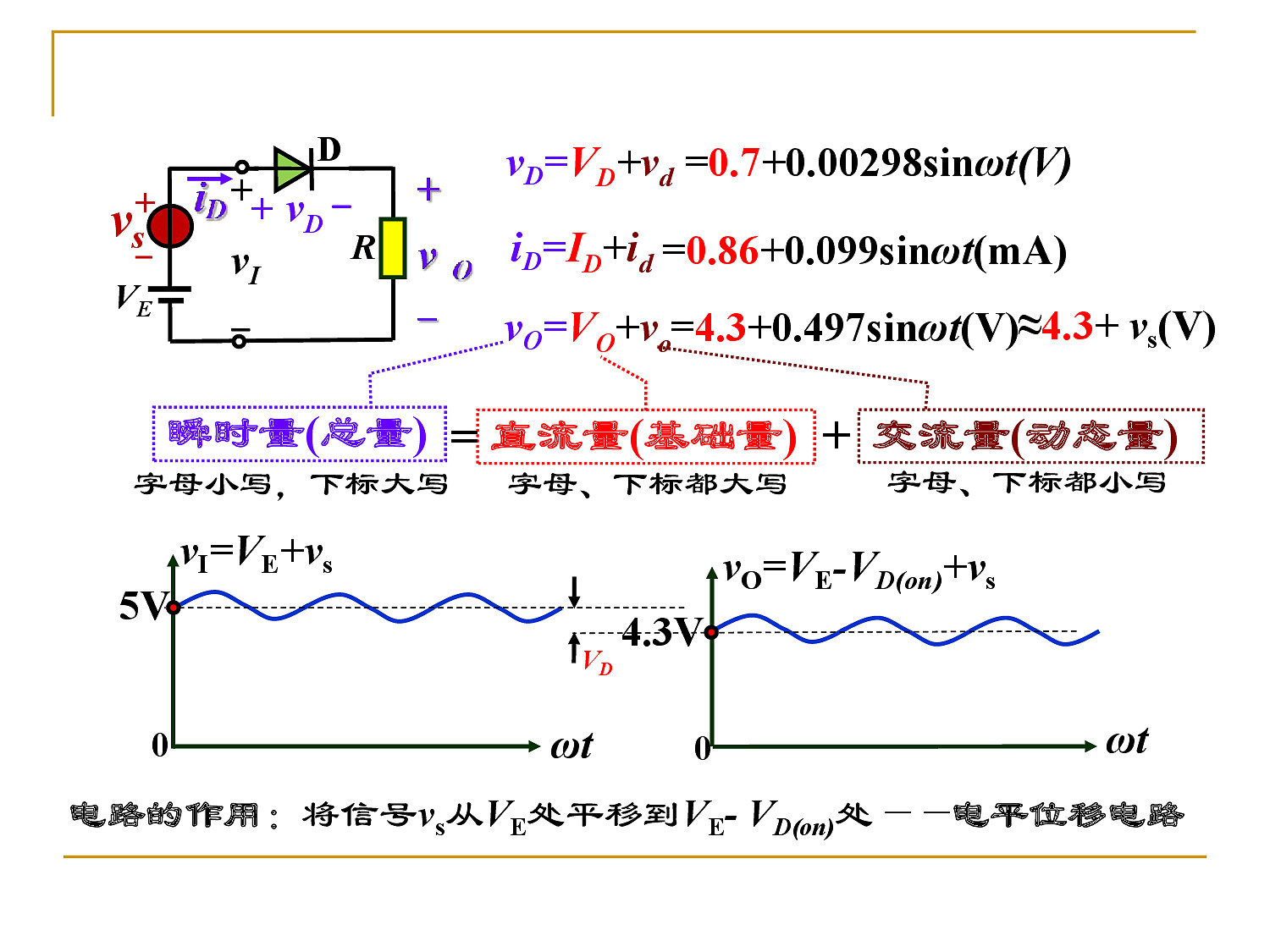
  • 图解分析法

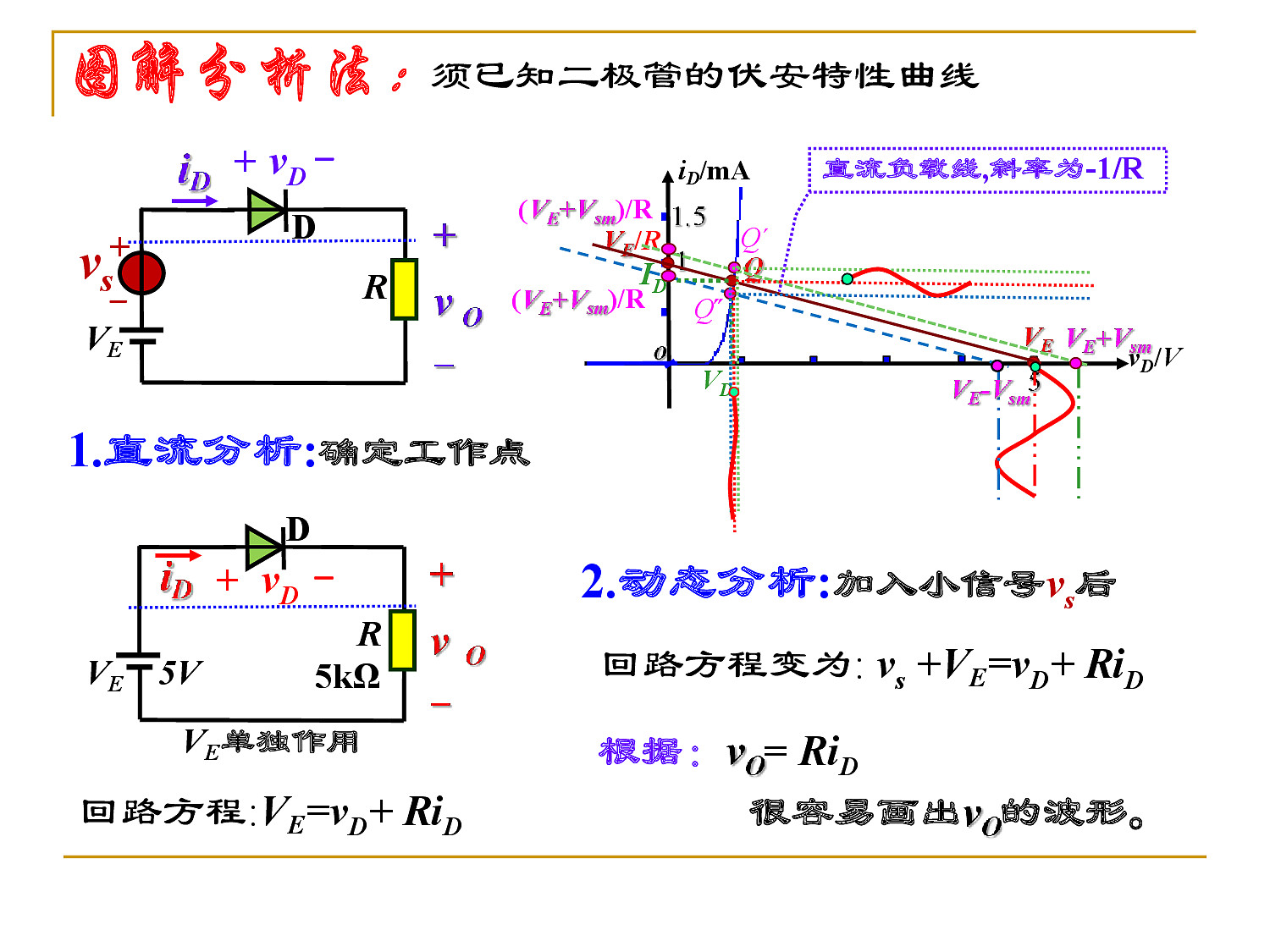
1.9 稳压二极管

稳压二极管由特殊工艺制作的二极管，可以在反向击穿状态下工作。（稳压管正常工作都处于反向击穿状态）

击穿电压 $V_{BR}$：反向击穿所需要的电压称为击穿电压（击穿原因：破坏原子中共价键的束缚，使自由电子空穴对数目急剧增加造成）

${击穿} = \begin{cases}热击穿_{（不可逆，必须避免）}：PN 结烧毁{i_D \cdot v_D > P_M}\\ 电击穿_{（可逆，可以利用）}：PN 结未破坏_{（断点/降压恢复）}{i_D \cdot v_D < P_M}\end{cases}$，$P_M$ 为 $PN$ 结耗散功率

若反向电流小于 $I_{Zmin}$，稳压管就会回到截止状态，即无法稳压；
若反向电流大于 $I_{Zmax}$，稳压管可能被热击穿。

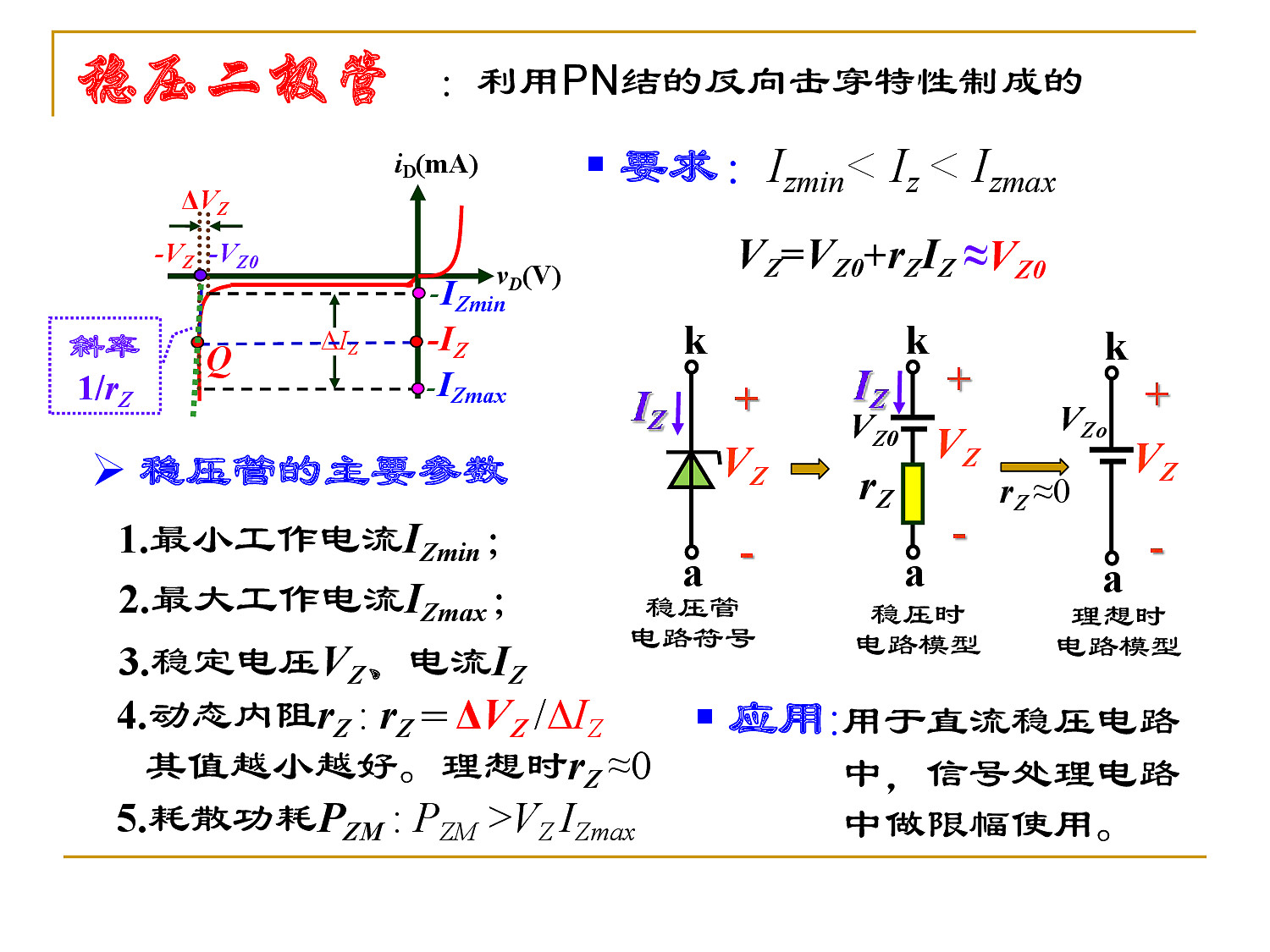
稳压管正常工作时，处于反向击穿状态，所以，电路中电压电流的参考方向与普通二极管相反，即反向击穿电压和反向电流都标注为正值。

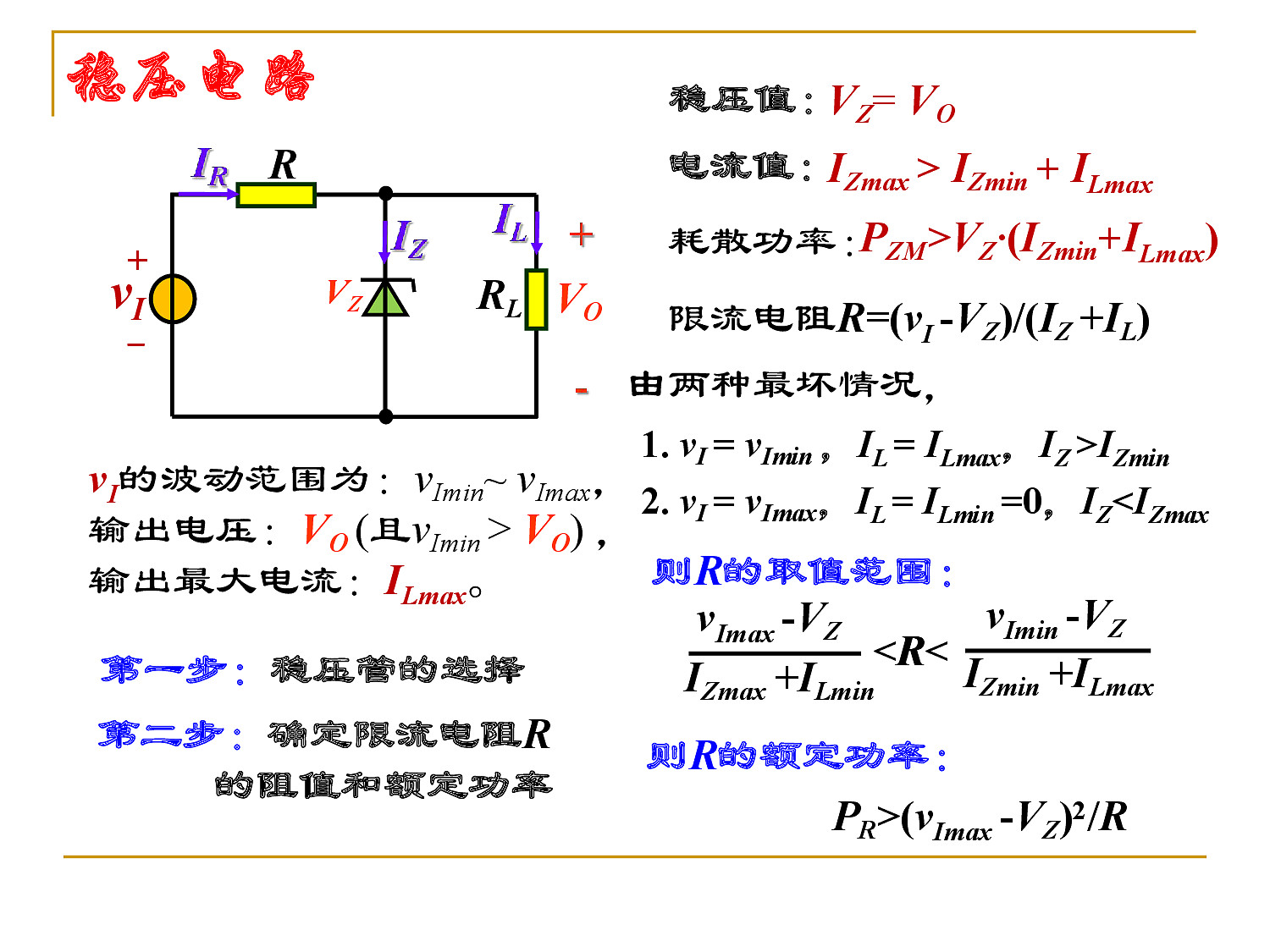
1.10 双极结型三极管结构

$BJT$

箭头标注在发射极上，表示发射结正偏时电流的实际方向，由 $P \to N$

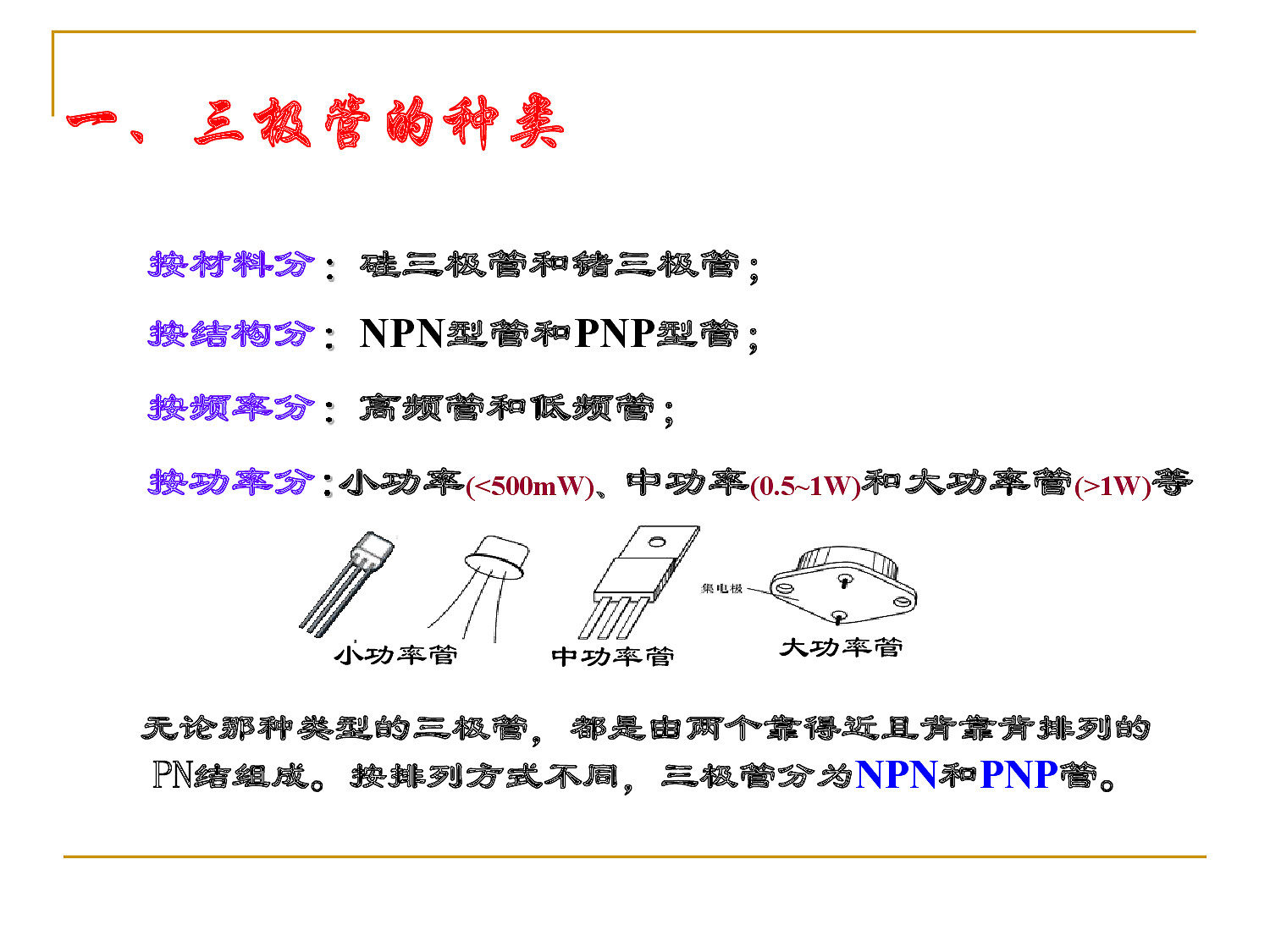
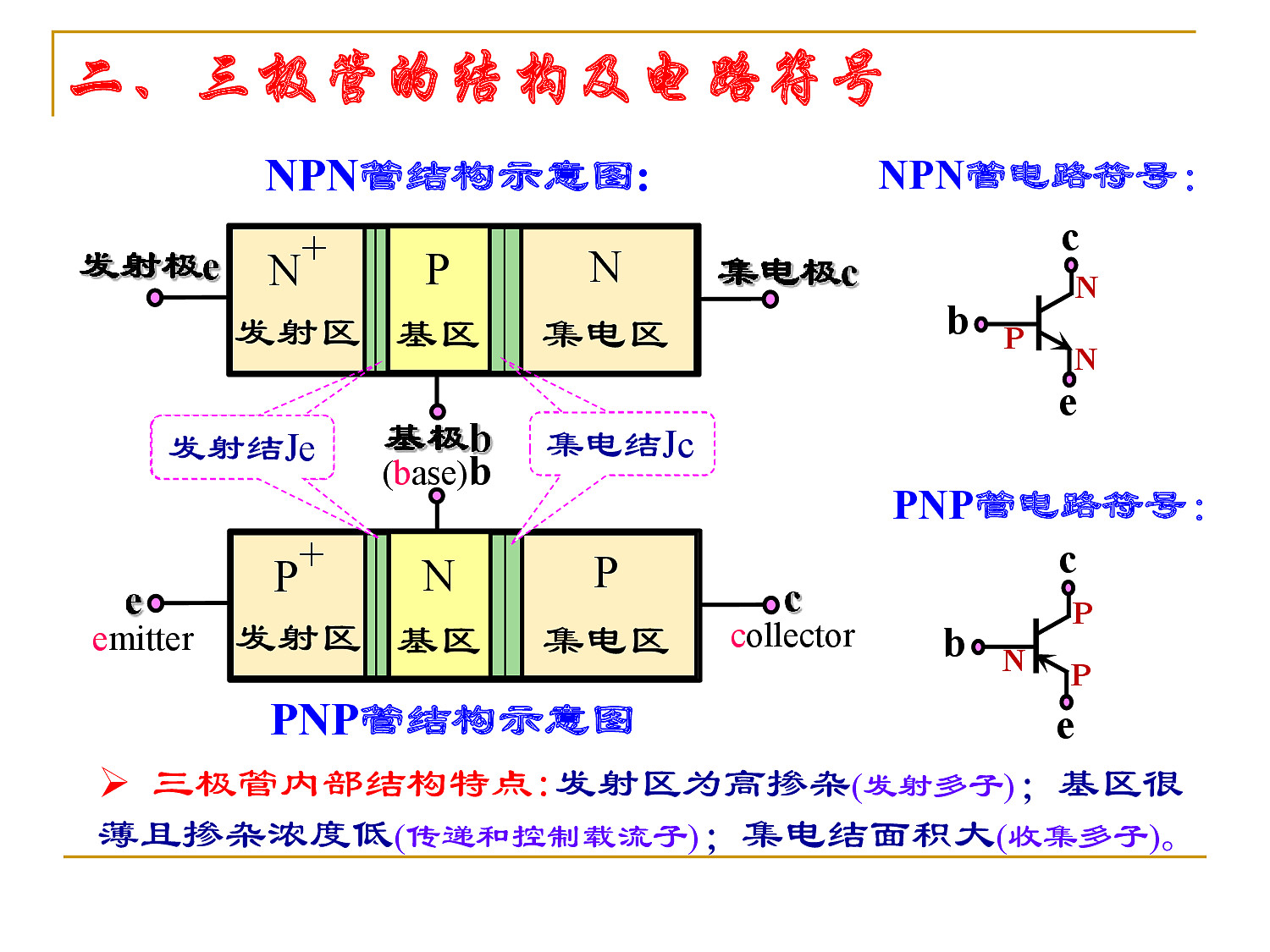
基区薄，减少基区复合概率，保证发射区载流子能扩散到集电结边界。

1.11 双极结型三极管导电原理

  • 三极管工作状态 & 外部条件：

    • 放大模式：发射结正偏，集电结反偏
    • 饱和模式：发射结正偏，集电结正偏
    • 截止模式：发射结反偏，集电结反偏

  • 放大模式（放大电流）


    - ${\large \alpha = \frac{收集电流}{发射电流} = \frac{i_{Cn} }{i_{En} } }$
    - ${\large \beta = \frac{收集电流}{复合电流} = \frac{i_{Cn} }{i_{En} - i_{Cn} } = \frac{i_{Cn} }{i_{Bn} } }$
    - ${I_C \approx \beta I_B} \approx \alpha I_E ,~ I_E \approx (1 + \beta)I_B$

  • 三极管的正向受控作用

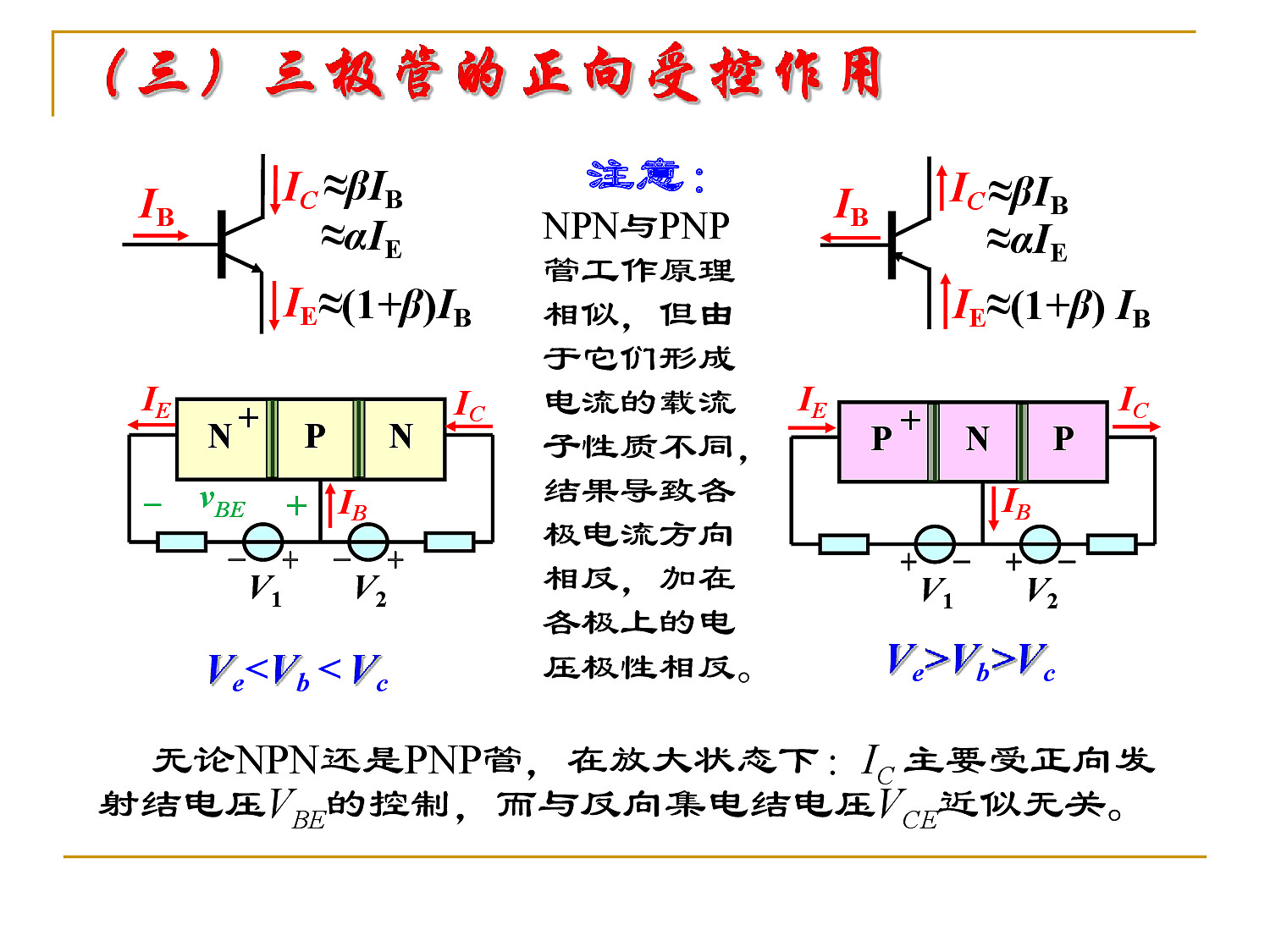
NPN，发射极电压最低

PNP，发射极电压最高

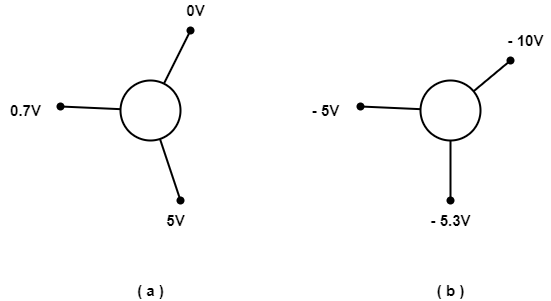
  • $(a) ~ \because V_{BE} = 0.7V, V_C = 5V ,~ \therefore V_E = 0V, V_B = 0.7V ,~ NPN硅管$
  • $(b) ~ \because V_{BE} = 0.3V, V_C = -10V ,~ \therefore V_E = -5V, V_B = -5.3V ,~ PNP锗管$

1.12 三极管伏安特性曲线

集电极不能做输入；基极不能做输出。

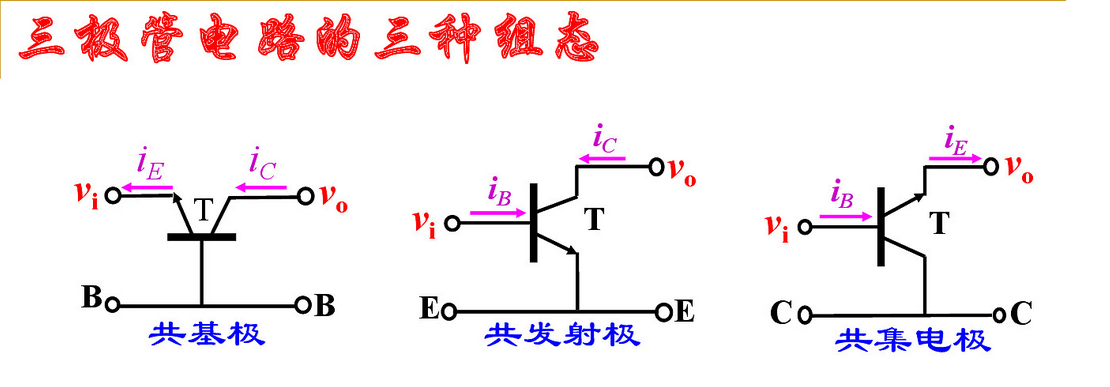
  • 共发射极

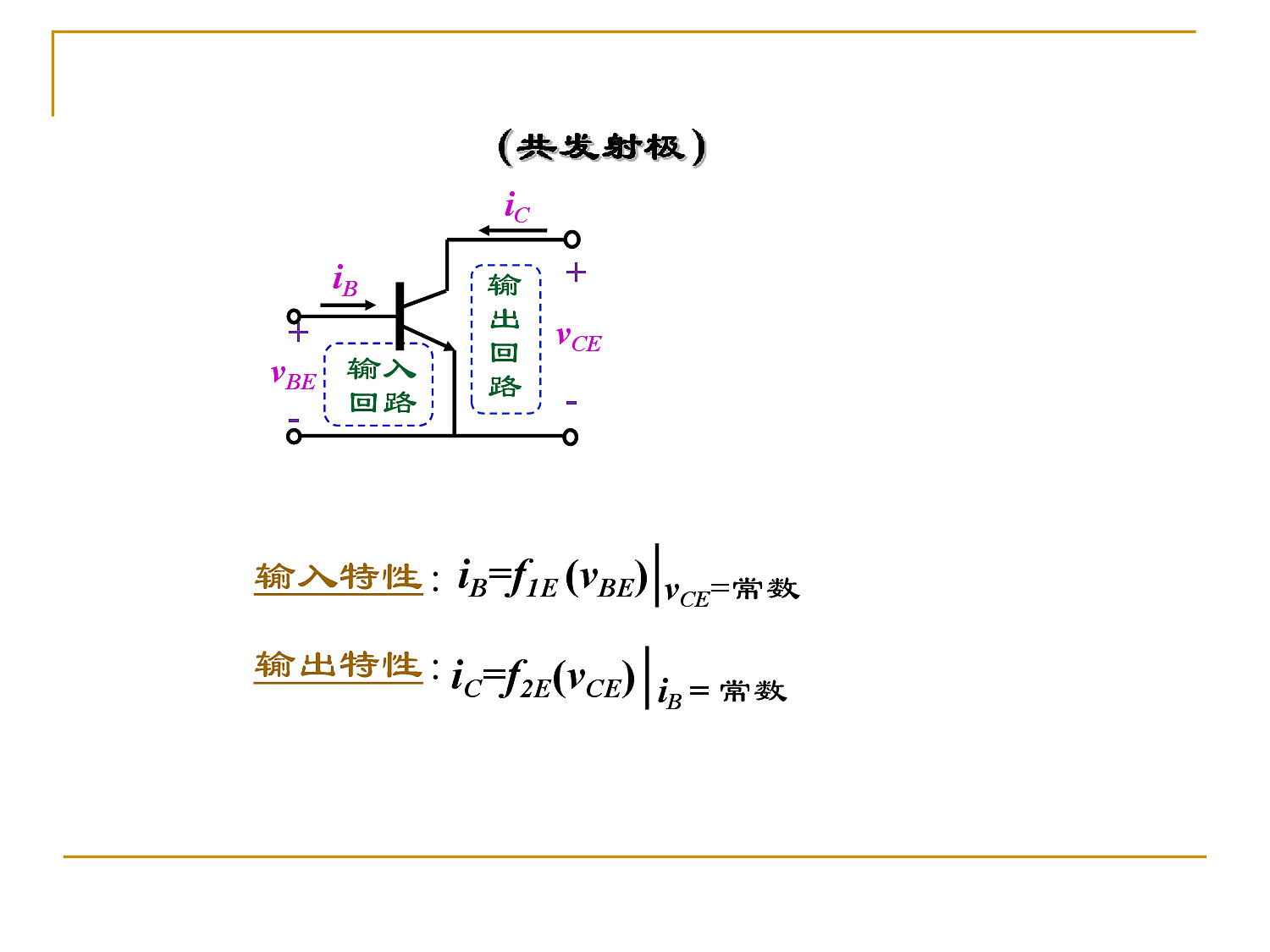
输入特性：$i_B = f(v_{BE})|_{v_{CE} = _{常数} }$

输出特性：$i_C = f(v_{CE})|_{i_B = _{常数} }$

  • 三极管的输入特性曲线

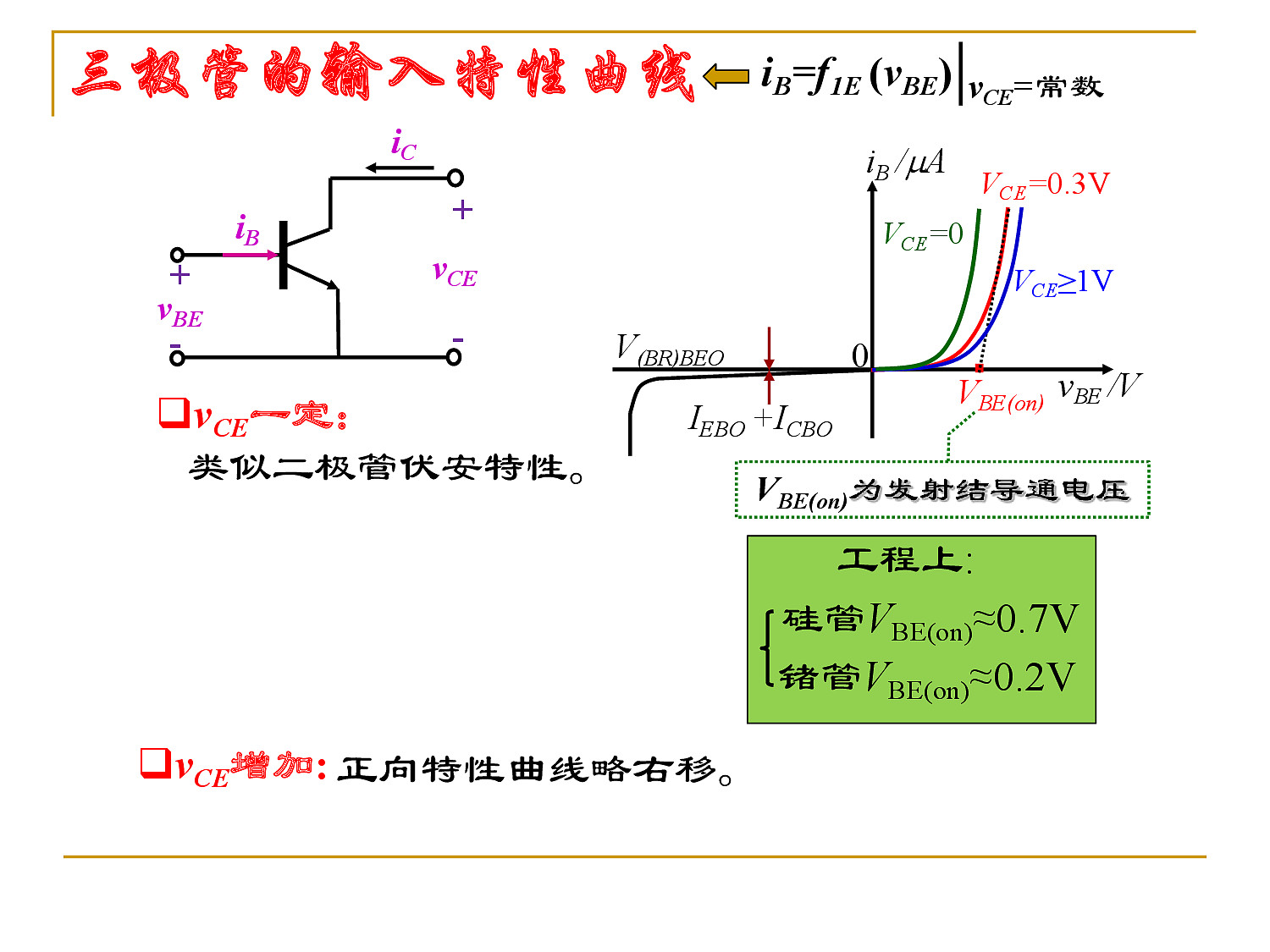
$V_{CE} < 1V$ 说明工作在饱和区

$V_{CE} \ge 1V$ 说明工作在放大区，$V_{BE}$ 为发射结导通电压

基区宽度调制效应：NPN：

$V_{CE} = V_{CB} + V_{BE}$，$V_{BE}$ 几乎不变，$V_{CE}$ 增大，$V_{CB}$增大，

CE 结电压变大（从发射极到集电极的引力越大，速率越快），

BC 结变宽，基区变窄（多子/自由电子很快到集电极，发射极的电子发射能力不行，电子供给不够，导致基极电子少了，电流小）。

$V_{CE}$ 越大，$V_{BE}$ 也要跟着变大，电流才能一致，或者在 $i_E$ 处增加一个电流源，使其电流恒定。

放大的本质：自由电子从发射极到集电极。$V_{BE} $不变，发射极发射的电子不变，$i_E$ 不变，$V_{CE}$增大，$i_C$增大，$i_B$自然就减小了，$i_{E} = i_{C} + i_{B}$

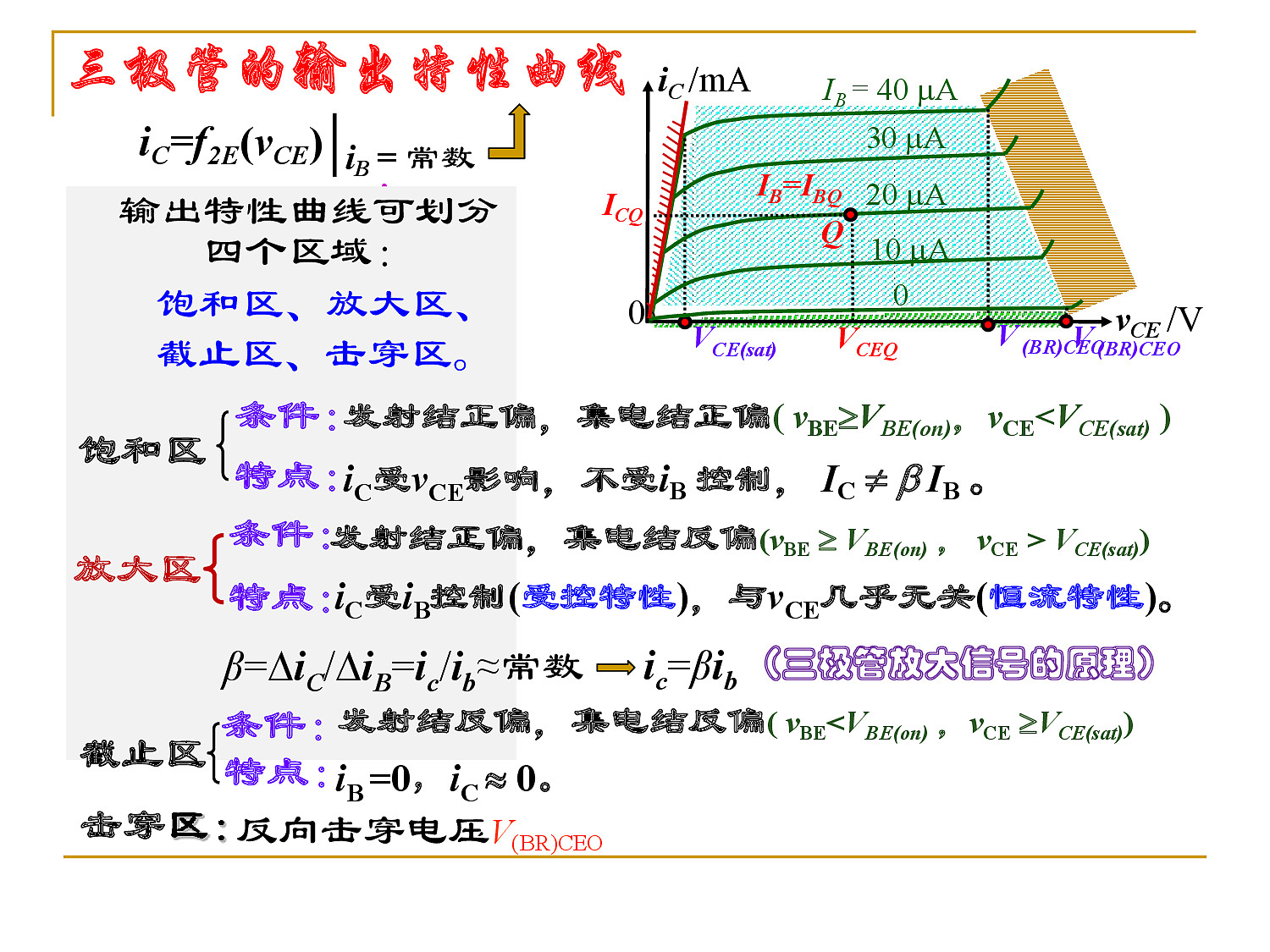
  • 三极管的输出特性曲线

输出特性曲线：饱和区、放大区、截止区、击穿区

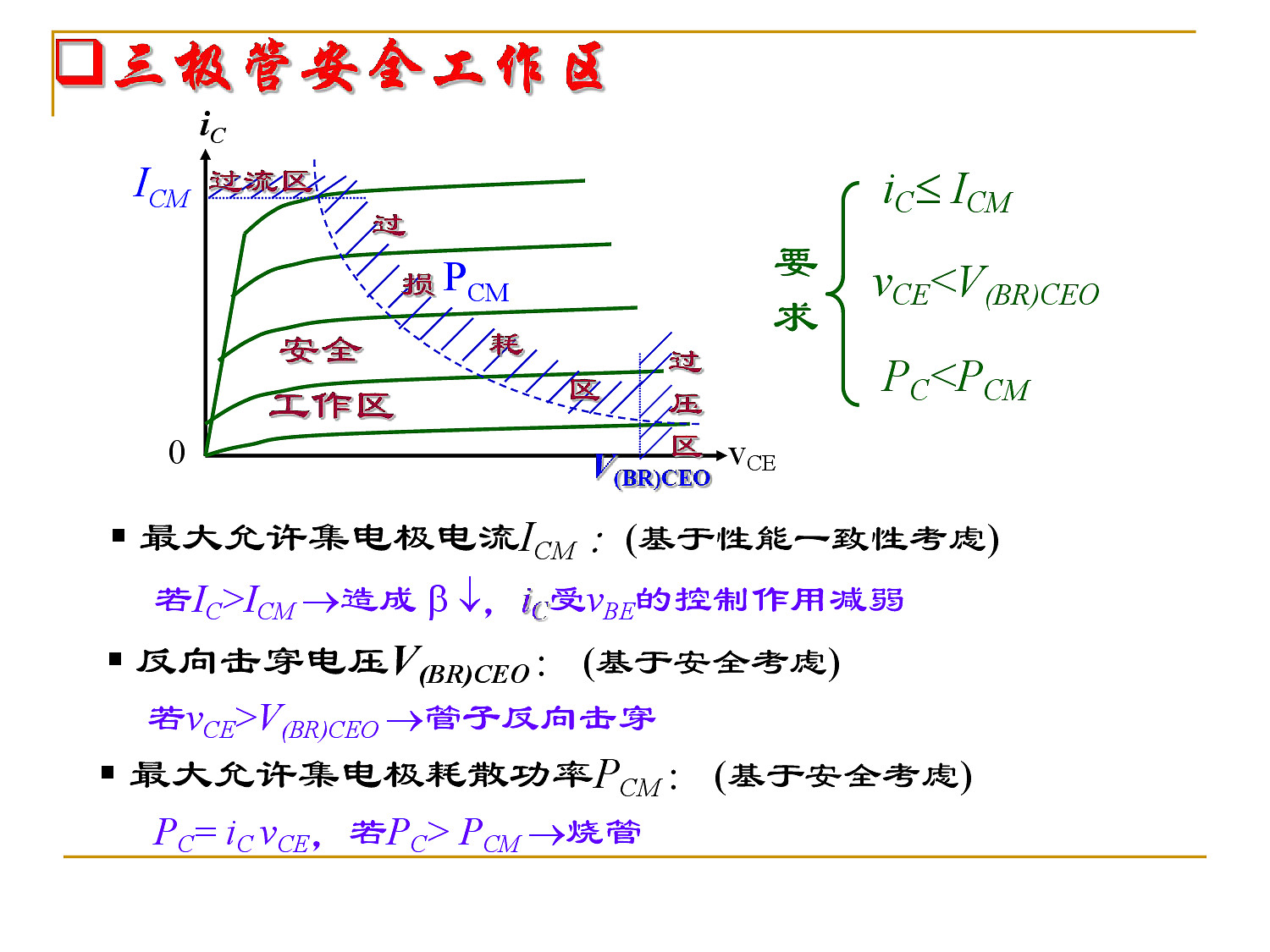
  • 三极管模型
  • 三极管的线性等效：直折线
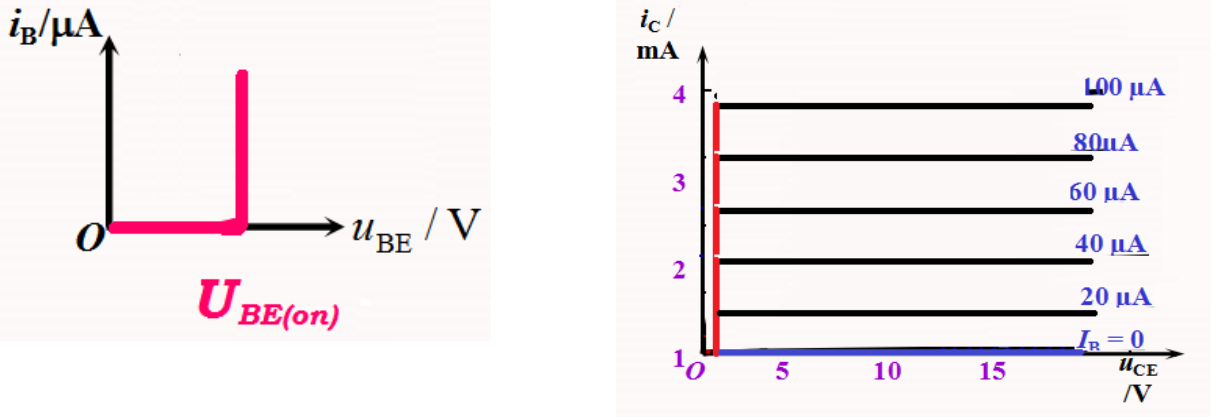
  • 饱和区直流电路简化模型

通常，饱和压降 $V_{CE(set)} \approx \begin{cases}0.3V & Si\ 0.1V & Ge\end{cases}$

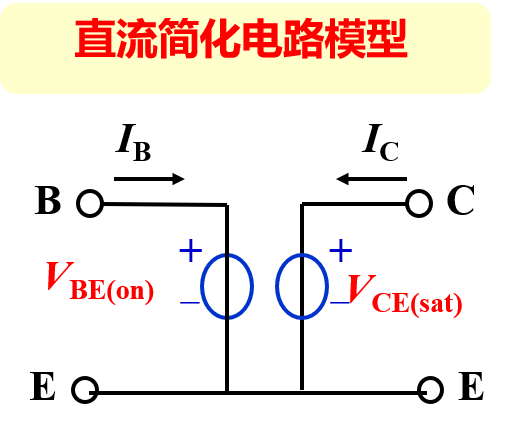
  • 放大区直流电路简化模型

发射结导通电压 $V_{BE(on)} = \begin{cases}0.7V & Si\ 0.2-0.3V & Ge\end{cases}$

  • 截止区直流电路简化模型
  • 例、静态工作点的近似计算（直折线模型）
graph TD
    subgraph "直流分析"
        step-s1[截止区]
        step-s2[放大区]
        step-s3[饱和区]
        step-1[画直流通路]
        step-2[看发射结是否导通]
        step-3[假设在放大区]
        step-4[否则在饱和区]

        step-1 --> step-2

        step-2 -->|no| step-s1
        step-2 -->|yes| step-3

        step-3 -->|yes| step-s2
        step-3 -->|no| step-4

        step-4 --> step-s3
    end

  • 放大区

    • $\begin{cases}V_{BE} \approx V_{BE(on)}\ I_C = \beta I_B\end{cases} \Rightarrow I_B、I_C、V_{CE}$
    • $NPN：V_{CE} > V_{CES}$，$PNP：V_{EC} > V_{ECS}$

  • 饱和区

    • $\begin{cases}V_{BE} \approx V_{BE(on)}\ V_{CE} \approx V_{CES}\end{cases}$

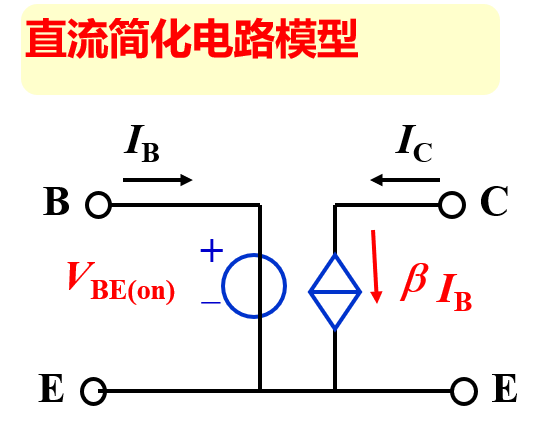
  • 三极管交流放大区小信号模型

$
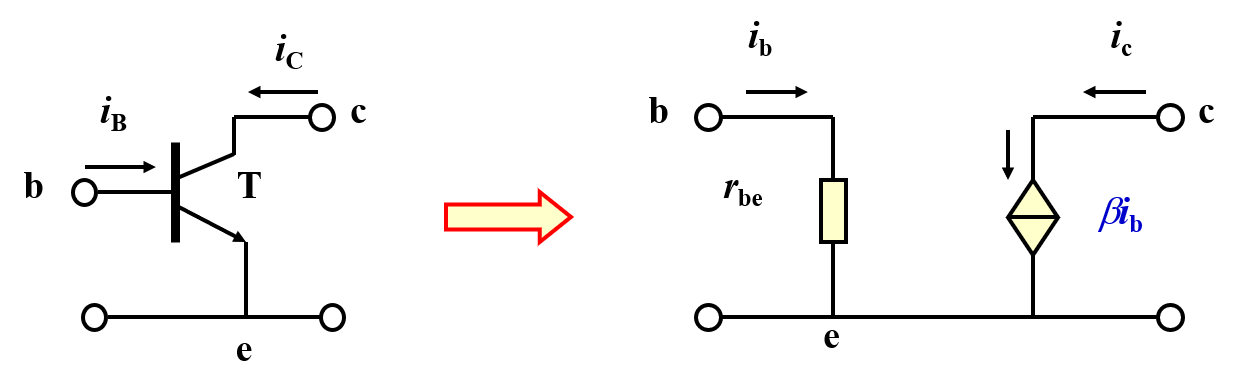
{\large r_{be} = r_{bb’} + r_{b’e} }\
{\large\quad~ \approx r_{bb’} + \frac{26(mV)}{I_{BQ} } }\
{\large\quad~ \approx r_{bb’} + (1 + \beta)\frac{26(mV)}{I_{EQ} } }\
{\large\quad~ \approx r_{bb’} + \beta\frac{26(mV)}{I_{CQ} } }\
$

注意：小信号电路模型只能用来分析叠加在 $Q$ 点上各交流量之间的相互关系，不能分析直流参量。

1.13 场效应管的结构及电路符号

PN 结处处反偏，场效应管工作

多子 $S \to D$

$i_D \approx K(v_{GS} - v_{GS(off)})^2$

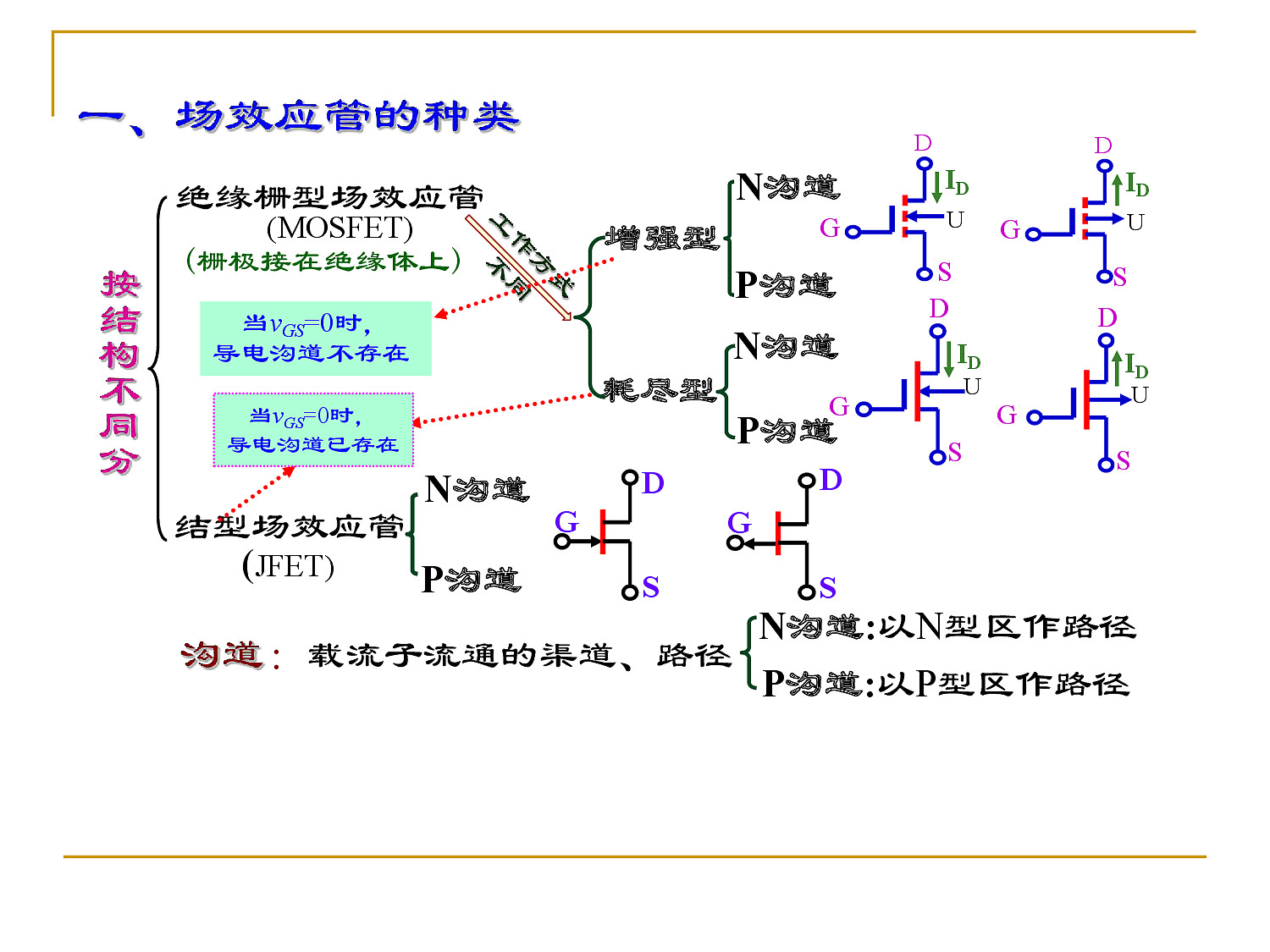
转移特性曲线：$i_D = I_{DO}(\frac{u_{GS} }{VGS(th)} - 1)^2$

  • 沟道：载流子流通的渠道、路径

    • N 沟道：以 N 型区作为路径
    • P 沟道：以 P 型区作为路径

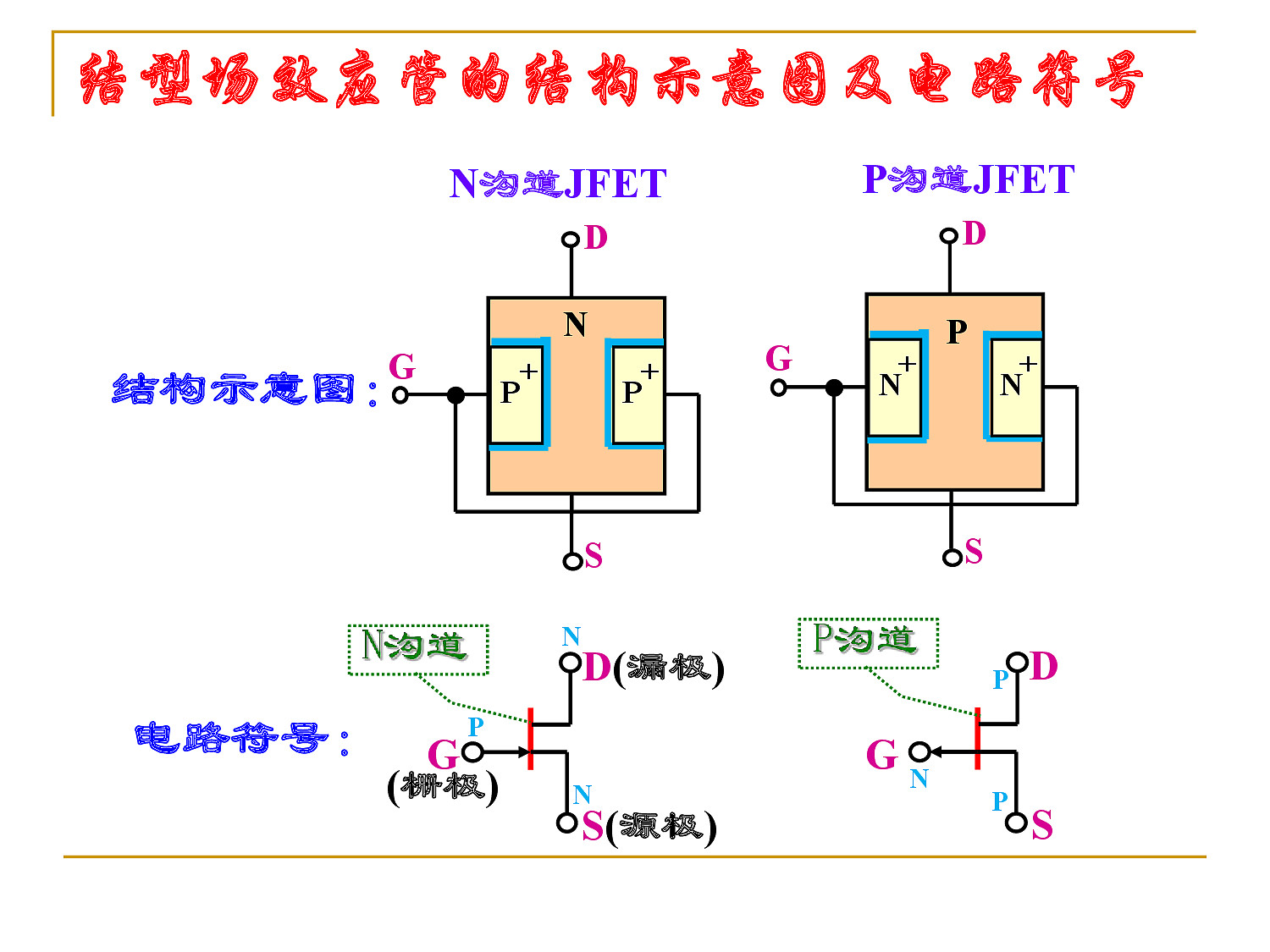
  • 结型场效应管的结构示意图及电路符号

  • 绝缘栅场效应管的结构示意图及电路符号

绝缘栅场效应管：也称为 金属-氧化物-半导体型场效应管，简称为 MOS管

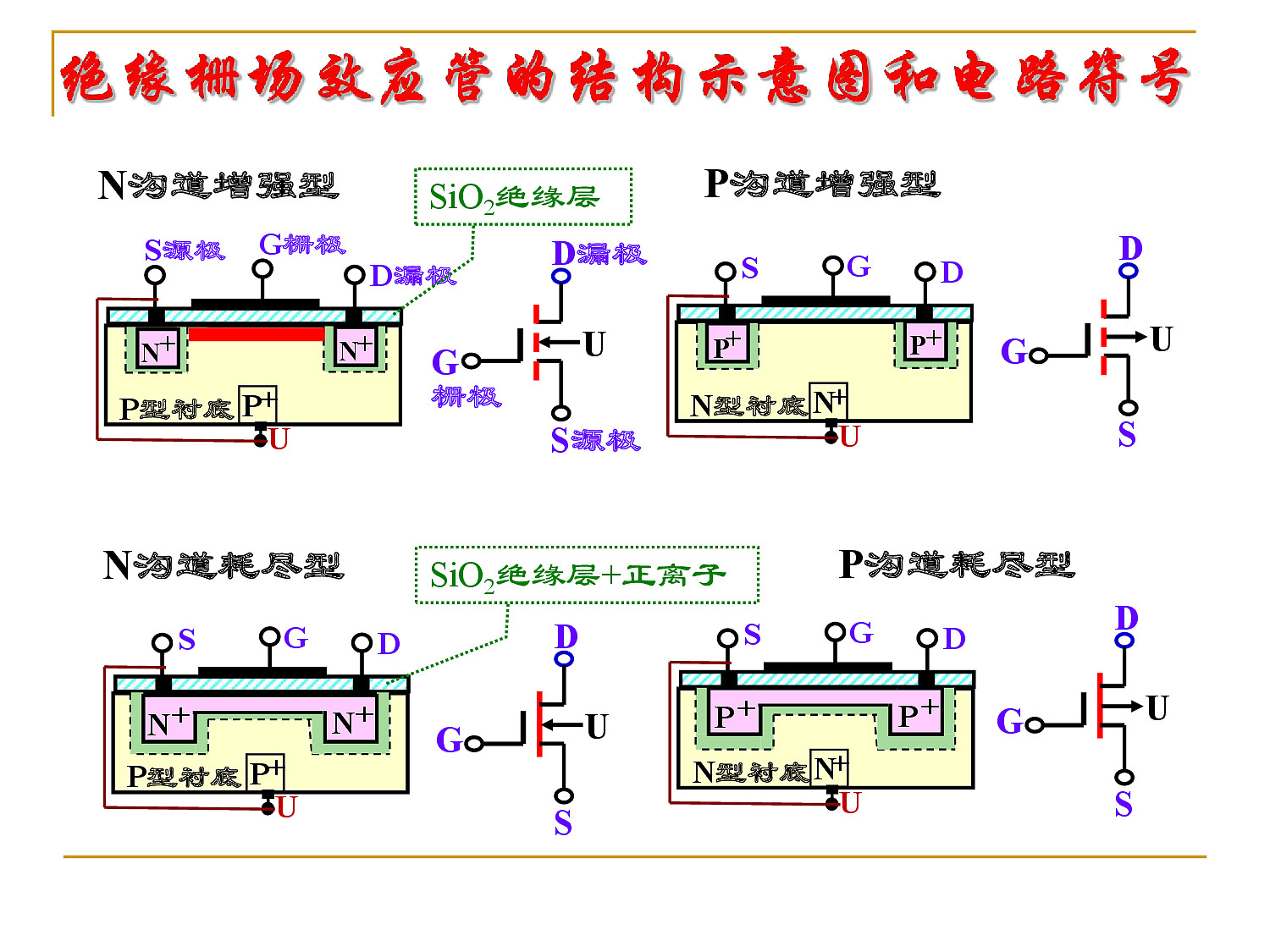
对 N 沟道增强型：

S 源极和 D 漏极之间要导电，需要通过栅极绝缘层下方称为沟道的区域。

一般 S 源极和 D 漏极均会和 P 型衬底之间形成 PN 结，导致 S 源极和 D 漏极无法导通。

要形成导电通道，必须在栅极加一定的电压，让沟道区域由 P 型衬底变成 N 型区

  • 另外

几个区：可变电阻区、横流区、夹断区、击穿区
也叫做：非饱和区、饱和区、截止区、击穿区

控制 G 栅极的电压，可以控制 S 源极和 D 漏极的电流，即控制 S 源极和 D 漏极的电阻，所以就得到一个电压控制的可变电阻器

  • 对于增强型：

$V_{GS(th)}$ 开启电压（th: threshold 阈值）

预夹断之后进入恒流区，$V_{GS}$ 可以控制 $i_D$

  • 对于耗尽型：

$V_{GS(off)}$ 关断电压

1.14 场效应管的工作原理及特性曲线

漏极不能做输入；栅极不能做输出。

简单来说，就是通过控制电压 $v_{GS}$ 和 $v_{DS}$ 控制电流 $v_{D}$，即受电压控制的电流源。

  • 转移特性曲线

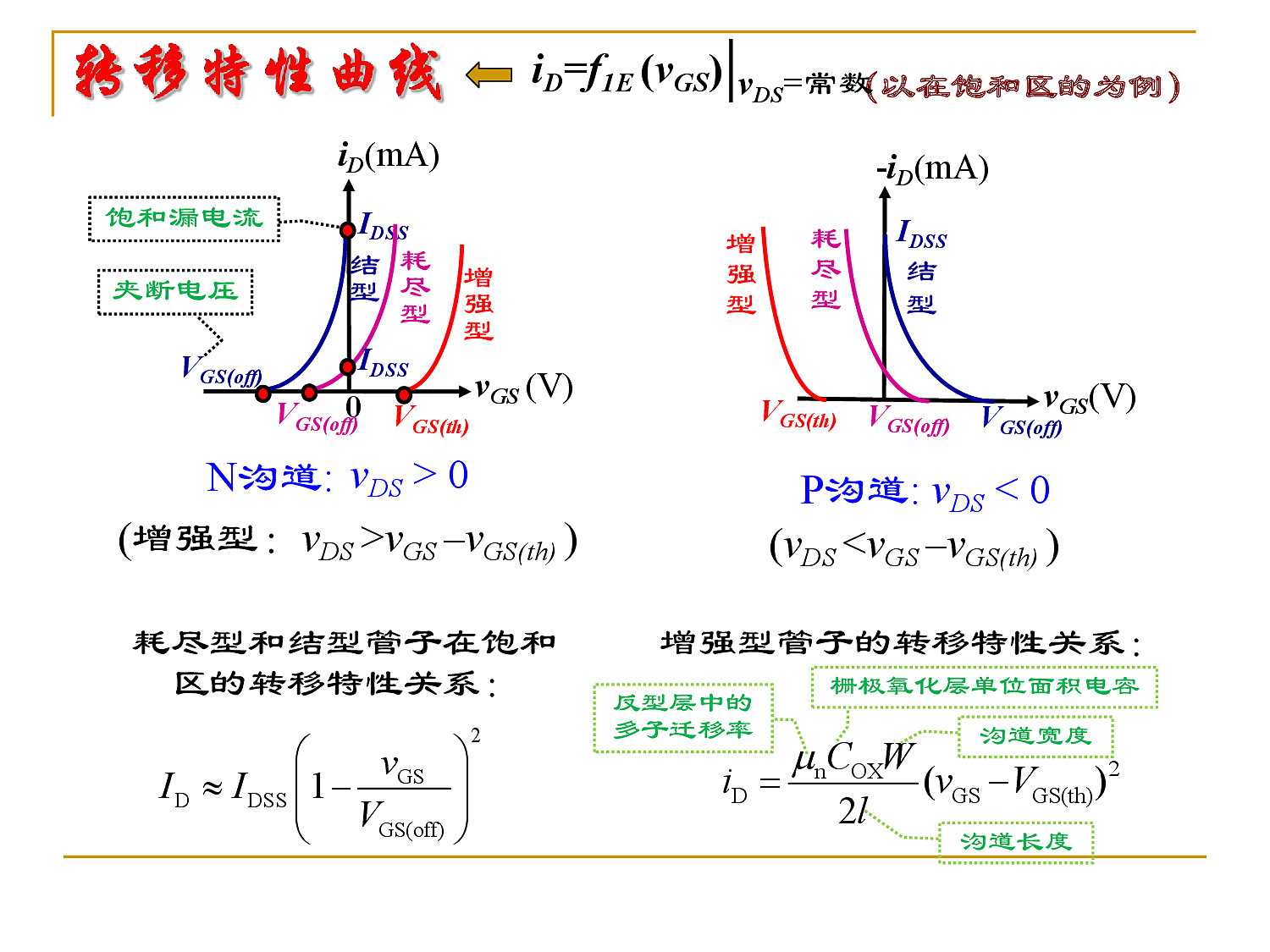
工作在饱和区的条件：

场效应管类型 条件
N 沟道结型 ${\large \begin{cases}v_{DS} > v_{GS} - v_{GS(off)}\\ v_{GS(off)} > v_{GS} > 0\end{cases} }$
N 沟道耗尽型 ${\large \begin{cases}v_{DS} > v_{GS} - v_{GS(off)}\\ v_{GSs} > v_{GS(off)}\end{cases} }$
N 沟道增强型 ${\large \begin{cases}v_{DS} > v_{GS} - v_{GS(th)}\\ v_{GS} > v_{GS(th)}\end{cases} }$

转移特性关系：

${\large i_D \approx K(v_{GS} - v_{GS(X)})^2 } ,~ X = th ~ or ~ off$

  • 输出特性曲线

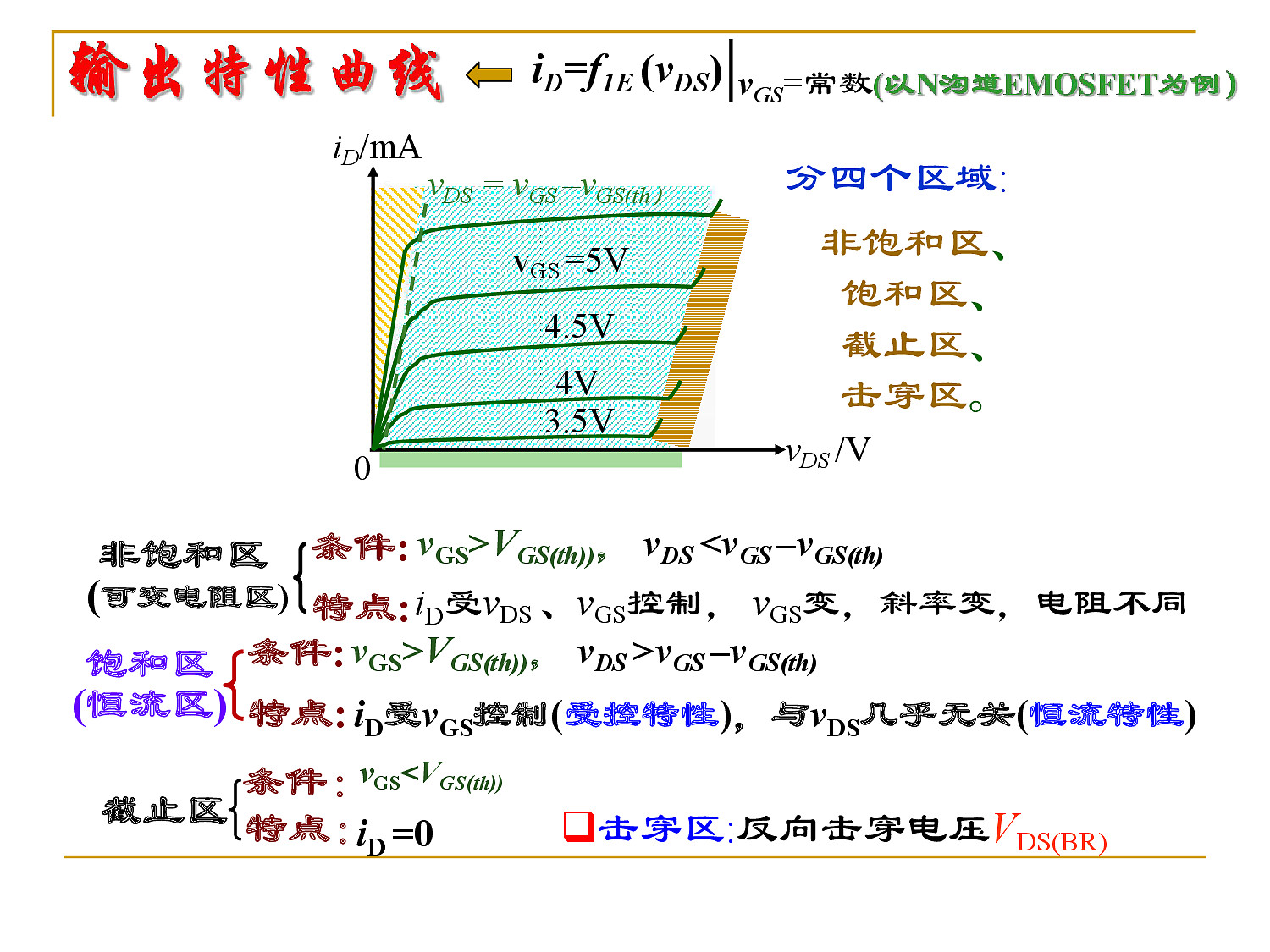
工作状态及其条件和特点：

工作状态 条件 特点
非饱和区
(可变电阻区)		 ${\large v_{GS} > v_{GS(th)},~ v_{DS} < v_{GS} - v_{GS(th)} }$ $i_d$ 受 $v_{GS}$ 和 $v_{DS}$ 控制
饱和区
(恒流区)		 ${\large v_{GS} > v_{GS(th)},~ v_{DS} > v_{GS} - v_{GS(th)} }$ $i_d$ 受 $v_{GS}$ 控制，与 $v_{DS}$ 几乎无关
截止区 ${\large v_{GS} < v_{GS(th)} }$ $i_d = 0$
击穿区 应尽量避免工作在该区域
  • 三极管 & 场效应管

三极管的放大区和场效应管的饱和区特点一样：

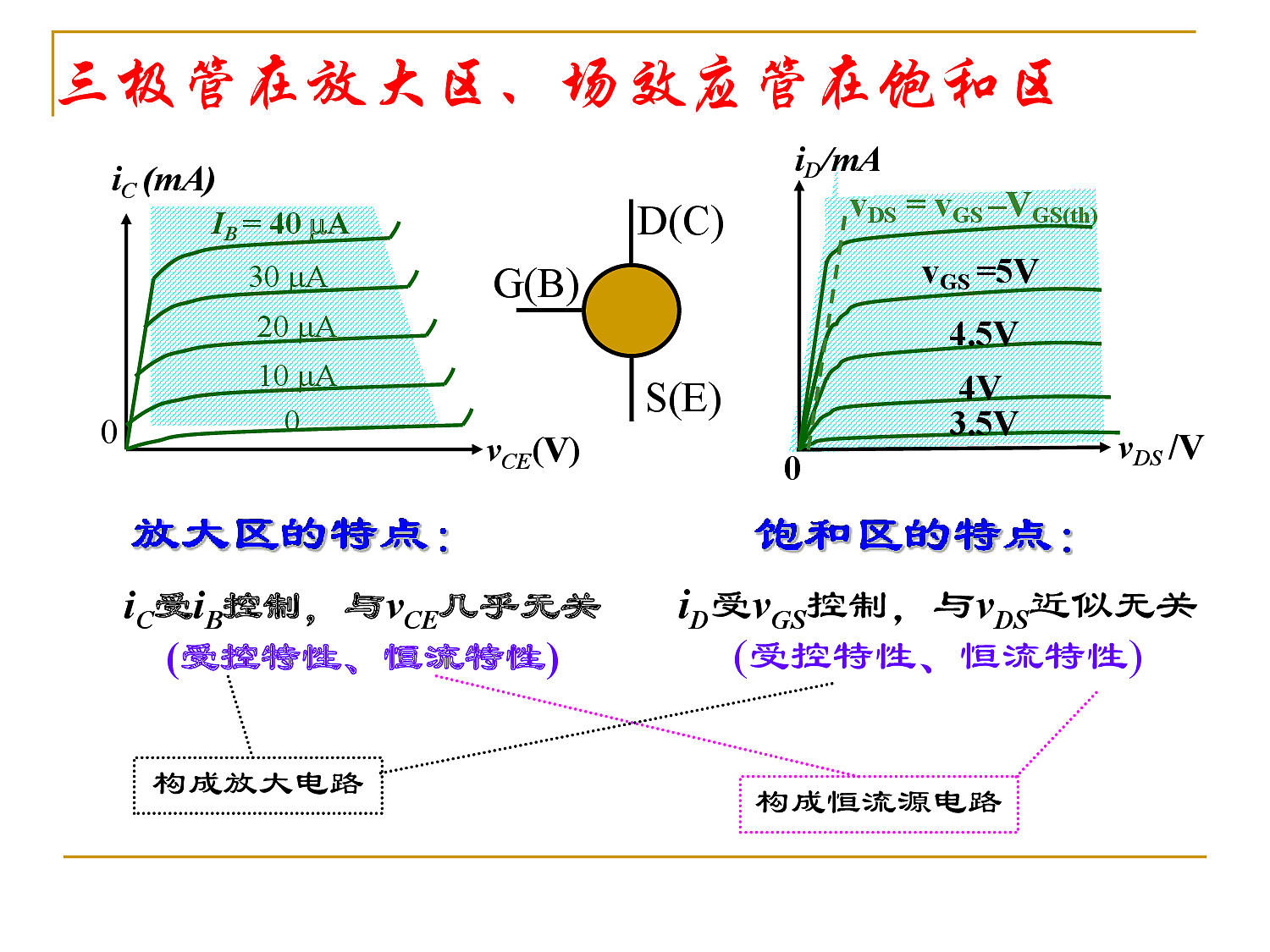
三极管是双极性电流控制型器件，场效应管是单极性电压控制型器件。

文章作者: hhhhmdzz
文章链接: https://hhhhmdzz.github.io/2022/06/29/di-1-zhang-ban-dao-ti-ji-chu-yuan-jian-yu-fei-xian-xing-dian-lu/
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 hhhhmdzz !
模电
赏
评论
  目录